Integrazione per serie di un'equazione differenziale
Dicembre 10th, 2021 | by Marcello Colozzo |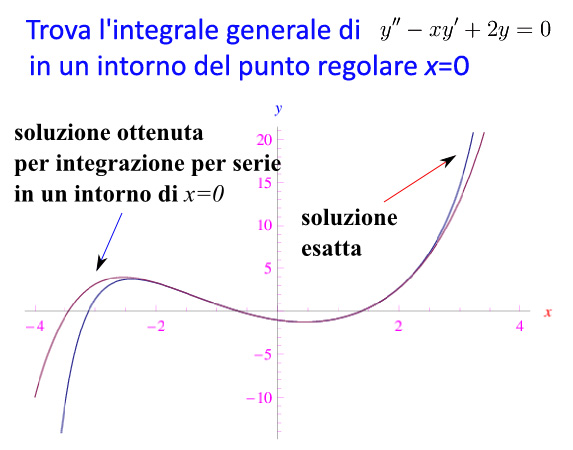
Studiamo il metodo di integrazione per serie di un'equazione differenziale lineare omogenea del secondo ordine, in un intorno di un punto ordinario/a> x0. A tale scopo, enunciamo senza dimostrare il teorema:
Teorema
L'integrale generale dell'equazione differenziale

in un intorno di un punto regolare x0, si esprime come
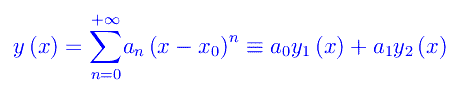
dove i coefficienti a0,a1 della serie di potenze al primo membro, sono costanti arbitrarie, mentre il sistema di integrali {y1(x),y2(x)} è linearmente indipendente.
Esercizio
Risolvere l'esercizio rappresentato in fig. 1.
Soluzione
Il punto x=0 è manifestamente un punto ordinario, per cui scriviamo l'espansione in serie di potenze dell'integrale generale:
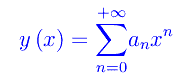
Ora non dobbiamo fare altro che derivare termine a termine per due volte, dopodiché immettere i rispettivi sviluppi in serie nell'equazione assegnata. Abbiamo:
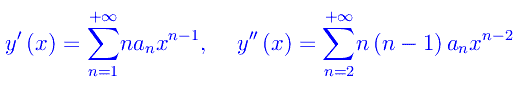
Per quanto detto:

Lo scopo del nostro procedimento è trovare una relazione di ricorrenza per i coefficienti della serie. Per fare ciò dobbiamo cercare di far comparire una sola sommatoria, cioè che parte dallo stesso valore iniziale (n=0, vedi ultima sommatoria a primo membro). Quindi nella prima, operiamo la sostituzione di indice:

dove nell'ultimo passaggio abbiamo rinominato l'indice muto n' in n. Ci rimane la sommatoria di mezzo (nella seconda delle equazione scritte più sopra). Qui non conviene la sostituzione n->n'+1, altrimenti ci ritroviamo con un fastidioso x^(n'+1). Osservando che compare n nel termine generico, possiamo tranquillamente scrivere:

Ne segue

cioè l'equazione di ricorrenza:

Ricordiamo che a0,a1 sono fissati ad arbitrio. Quindi

Precisamente, i coefficienti con n pari >= 4 sono tutti nulli. Abbiamo

Ordinando i vari termini:

Quindi l'integrale generale in un intorno di x=0, è dato da:

essendo

due integrali particolari linearmente indipendenti. In fig. 1 riportiamo il grafico della soluzione ottenuta per serie (con a0=-1,a1=-1) confrontata con il grafico della soluzione esatta ottenuta con Mathematica. Notiamo incidentalmente, che essendo la soluzione esatta non elementarmente esprimibile, Mathematica la ricava utillizzando alcune funzioni speciali (non elementarmente esprimibili).



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











