» Esercizi svolti di Matematica e Fisica

Punti ordinari e punti singolari di un'equazione differenziale

Dicembre 9th, 2021 | by Marcello Colozzo |

---

Dopo questa lunga premessa, riprendiamo l'equazione differenziale del secondo ordine:

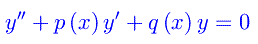
dove p(x) e q(x) sono funzioni assegnate e definite in X sottoinsieme di R.

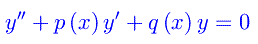
Definizione 1

Se p(x) e q(x) sono analitiche in X, ogni punto di tale insieme si dice punto ordinario dell' equazione differenziale scritta sopra. Denotando con D(X) il derivato di X, se in

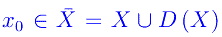
una delle predette funzioni non è analitica, diremo che x₀ è un punto singolare dell'equazione.

I punti singolari si classificano secondo la seguente definizione:

Definizione 2
Un punto singolare x₀ regolare se le funzioni

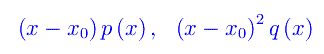
sono analitiche. Nel caso contrario, x₀ è un punto singolare non regolare.

Esempio
Consideriamo l'equazione differenziale

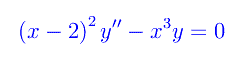
che può essere scritta come

Ne segue

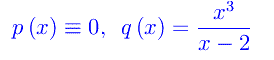
Il punto x₀=2 è manifestamente un punto singolare. Per classificarlo procediamo come definizione:

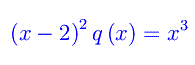
che è analitica in R. Ne concludiamo che si tratta di un punto singolare regolare.

Articoli correlati