La funzione zeta di Riemann: dalla z-rappresentazione alla w-rappresentazione

Novembre 8th, 2021 | by Marcello Colozzo |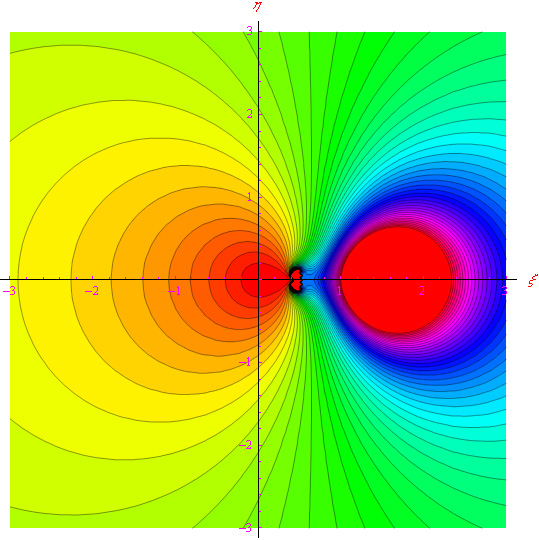

funzione zeta di riemannn,retta critica,punto all'infinito
Fig. 1

In fig. 1 sono suggestivamente tracciate alcune curve di livello (utilizzando l'istruzione ContourPlot di Mathematica) della funzione zeta di Riemann dopo aver eseguito il cambio di variabile


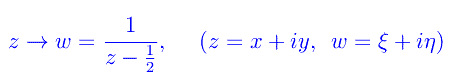
che proietta all'infinito il punto z=1/2, mentre la retta critica

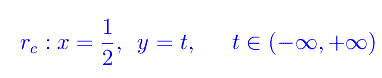
diviene il luogo di rappresentazione parametrica:

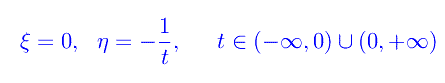
vale a dire l'asse immaginario privato dell'origine. La striscia critica è

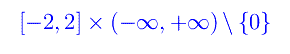
e la simmetria degli zeri viene conservata. In particolare gli infiniti zeri che cadono sulla retta critica, nella w-rappresentazione si addensano intorno all'origine ξ=0,η=0 che rappresenta manifestamente il punto all'infinito della z-rappresentazione.

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , ,

Articoli correlati

Commenta l'esercizio