Somma delle lunghezze di due perpendicolari

Novembre 2nd, 2021 | by Marcello Colozzo |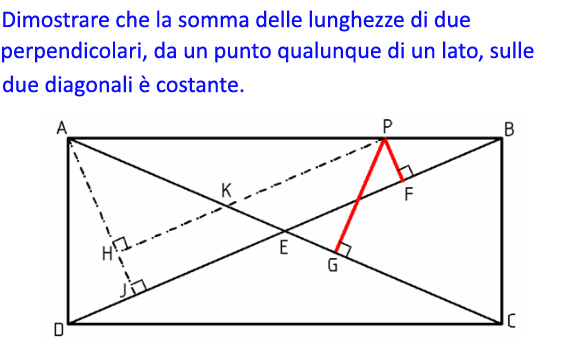

rettangolo,diagonali,perpendicolari
Fig. 1

Esercizi di Geometria elaborati dell'ing. Giorgio Bertucelli.

Esercizio

Dimostrare che la somma delle lunghezze di due perpendicolari, da un punto qualunque di un lato, sulle due diagonali è costante (fig. 1).

Soluzione

Da un punto P del lato AB si traccino le perpendicolari PG e PF. Dal vertice A si tracci la perpendicolare AJ e dal punto P si tracci la perpendicolare PH. È chiaramente


ma è anche PH\\BD. Quindi abbiamo


Poiché

abbiamo


così per transitività scriveremo

Nel triangolo APH si ha


Poichè

i triangoli AHK e PGK sono identici. Quindi

e sommando otteremo:

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , ,

Articoli correlati

Commenta l'esercizio