Configurazioni lontane dall'equilibrio

Ottobre 23rd, 2021 | by Marcello Colozzo |

mappa logistica,caos deterministico — **Fig. 1**

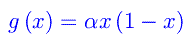
dove α > 0 è un parametro libero. Computazionalmente, vediamo che per 0 < α <= 3 abbiamo un fixed point come mostrato nel grafico di fig.

Esistono dei valori caratteristici del predetto parametro, in corrispondenza dei quali si verifica la comparsa di fixed points repulsivi. Ad esempio, per α=3.1, troviamo due punti fissi repulsivi di periodo 2 come mostrato in fig.

Per α=3.45 abbiamo un raddoppio del periodo

Per α=4 l'insieme dei punti periodici repulsivi è denso in [0,1], come mostrato in fig.

In altri termini, per tale valore l'insieme dei punti repulsivi ha la potenza del continuo (ciò è una conseguenza di una proprietà topologica della mappa g). Un tale sistema è ergodico e caotico. In fig.1 riportiamo il numero di punti repulsivi in funzione del parametro α. Si notino le transizioni di cui sopra: per α > 4 l'insieme dei fixed points ha la potenza del continuo. Il primo valore caotico è α=3.56. C'è tuttavia una finestra di stabilità per α di poco superiore a 3.8.

No TweetBacks yet. (Be the first to Tweet this post)