Moto di due dischi nello stesso piano
Settembre 20th, 2021 | by Marcello Colozzo |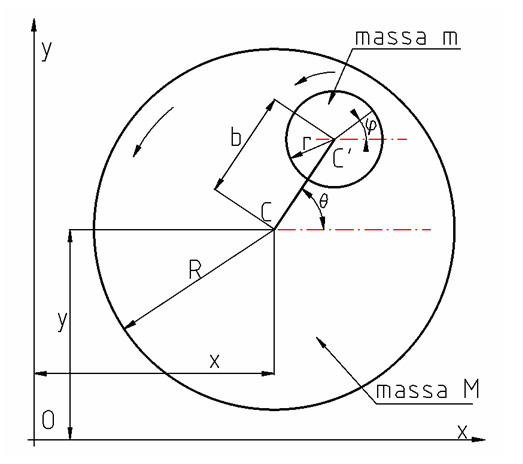
Esercizio
Un disco di massa M può muoversi su un piano Cxy senza attrito. Un disco più piccolo, di massa m, è collegato al disco più grande (fig. 1). Descrivere il moto e determinarne le costanti
Soluzione
Il centro di massa C' ha coordinate

e componenti di velocità

Quindi l'energia cinetica totale del sistema composto dai due dischi è

La lagrangiana è

Ricordando le equazioni di Lagrange, scriviamo

oppure

Inoltre

Per esplicitare l'altra equazione

dobbiamo calcolare le derivate parziali:

Quindi

L'equazione del moto è

Ne segue che il moto è governato dalle equazioni:

Poiché V=0 e T+V=cost in quanto non ci sono forze esterne, il sistema conserva l'energia cinetica. La conservazione del momento angolare richiede che


No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











