La ricorsività secondo Hofstadter
Maggio 28th, 2021 | by Marcello Colozzo |
Nel best seller Goedel, Escher, Bach, un'eterna ghirlanda brillante l'autore (Douglas Hofstadter) espone in maniera originale l'importante nozione di ricorsività. Per essere più specifici, a pag. 144 (ed. Adelphi) si parla di "toccare il fondo". Ciò significa assegnare il valore iniziale di una successione ricorsivamente definita. Per fissare le idee sia data la successione:
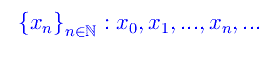
La definizione ricorsiva consiste nell'assegnare una funzione reale f(x) tale che
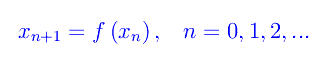
ed è chiaro che la successione è univocamente determinata dal valore iniziale x0. È facile persuadersi che ciò equivale nel continuo ad assegnare un problema di Cauchy relativo a un'equazione differenziale ordinaria del primo ordine autonoma. Più precisamente, definiamo la funzione reale:
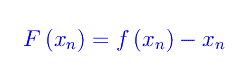
Segue

avendo introdotto la variabile "tempo" opportunatamente campionata (Δt=1). Passando al continuo:
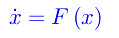
ovvero un'equazione differenziale del primo ordine autonoma. Per una qualuque f(x) lipchitziana, esiste ed è unica la soluzione del problema di Cauchy:

er quanto visto, le successioni ricorsivamente definite sono particolari funzioni da N a R, e rappresentano la controparte discreta di processi fisici governati da equazioni differenziali autonome. Di contro, Hofstadter si riferisce a successioni da N a N, come ad esempio quella che denota con G(n). Noi preferiamo utilizzare una notazione differente. Precisamente:

ove il termine n-esimo è così definito:

Esplicitiamo alcuni valori:

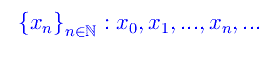
Tags: hofstadter, ricorsività
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











