» Esercizi svolti di Matematica e Fisica

Esercizio svolto sullo spazio duale. Ricerca della base duale

Maggio 22nd, 2021 | by Marcello Colozzo |

---

Come esempio numerico della lezione precedente consideriamo lo spazio vettoriale R². La base canonica è

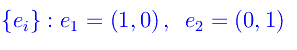
per cui

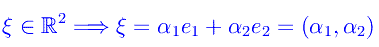
Consideriamo la seguente applicazione da R² a R

illustrata in fig. 1. Mostriamo che è un omomorfismo, quindi un funzionale lineare:

Ne segue che si tratta di un elemento dello spazio duale R^2*. La base duale rispetto alla base canonica è:

È conveniente utilizzare il formalismo delle matrici, rappresentando i vettori della base canonica con vettori colonna:

e i vettori della base duale con vettori riga:

Un qualunque vettore dello spazio duale si scrive come combinazione lineare dei vettori della base duale:

dove φ(e_i) sono le componenti di φ nella predetta base. Nel formalismo delle matrici

Osservando che un qualunque vettore di R² ha la rappresentazione matriciale

si ha:

Tags: base duale, esercizi svolti, spazio duale

Articoli correlati