Spazio duale di uno spazio vettoriale. Base duale

Maggio 21st, 2021 | by Marcello Colozzo |

Sia V uno spazio vettoriale su un campo K. Dal momento che quest'ultimo può essere considerato come spazio vettoriale su K medesimo, fissiamo l'attenzione su Hom(V,K) i cui elementi sono gli omomorfismi da V a K:

che si chiamano funzionali lineari Come è noto, introducendo le leggi di composizione (addizione di vettori, moltiplicazione di uno scalare per un vettore):

e relativi assiomi, Hom(V,K) assume la struttura di spazio vettoriale su K.
Definizione
Lo spazio vettoriale Hom(V,K) si dice spazio duale e si indica con V^*

Come sappiamo

Cioè V e V^* sono isodimensionali, e per un noto teorema segue che sono isomorfi. Inoltre, se {e_i} è una base di V:

Introduciamo n funzionali lineari così definiti:

Proposizione
{φ_i} è una base di V^*.

Dim.

Nell'equazione scritta più sopra possiamo esprimere

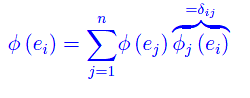
per cui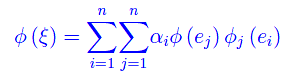

D'altra parte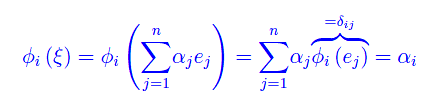

Quindi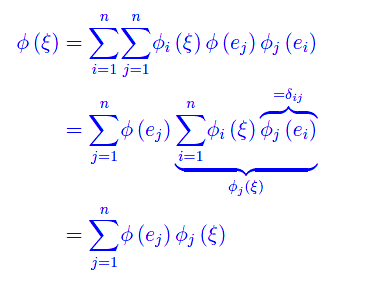

Cioè

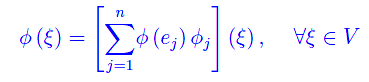
onde l'asserto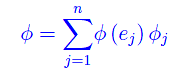

Definizione
La base {φ_i}} si dice base duale rispetto alla base {e_i}}.
Dalla proposizione appena dimostrata, segue che le φ(e_j) sono le componenti del funzionale lineare φ nella base duale.

No TweetBacks yet. (Be the first to Tweet this post)