Il vuoto quanto-meccanico

Maggio 7th, 2021 | by Marcello Colozzo |

vuoto quanto-meccanico,vuoto quantistico,spazio di hilbert

Sia S_q^N un sistema quanto-meccanico composto da N particelle distinguibili. Al variare di N nell'insieme N degli interi naturali, abbiamo una successione di spazi di Hilbert:

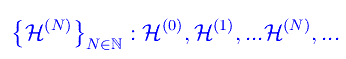
Fisicamente, ciò equivale a considerare un unico sistema il cui numero di particelle è variabile. Per definizione, uno spazio di Hilbert è uno spazio vettoriale definito sul campo complesso C, in cui è definito un prodotto hermitiano (cercate nel blog), e tale spazio risulta infinito-dimensionale. Quindi

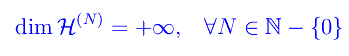
Per N=0 abbiamo un sistema quantistico privo di particelle. Chiamiamo vuoto quanto-meccanico o semplicemente vuoto, tale sistema. Per esplicitare il corrispondente sistema quantistico, consideriamo il caso N=1, ossia un sistema costituito da una sola particella in regime nonrelativistico che possiamo supporre (senza perdita di generalità) priva di spin. Come ben sappiamo, lo spazio di Hilbert è

cioè lo spazio funzionale i cui elementi sono

Si ricordi che tale spazio è completo (ogni successione di Cauchy converge a un elemento dello spazio medesimo) ed è separabile. La separabilità è essenziale in meccanica quantistica, giacché un noto teorema garantisce l'esistenza di basi ortonormali. Nel caso in esame, si pensi ai polinomi di Hermite o a un sistema di autovettori di un opportuno operatore essenzialmente autoaggiunto dotato di spettro puramente discreto.
Per definizione:

Questa posizione potrebbe apparire impropria, poiché uno spazio di Hilbert è necessariamente infinito-dimensionale, per cui ci sembra più adatta la denominazione spazio unitario. Segue manifestamente

ove le virgolette ci avvertono che non ha senso parlare di ortogonalità, per cui c'è solo la normalizzazione <0|0>=1. Da tutto questo formalismo la definizione di vuoto appare ben posta.

No TweetBacks yet. (Be the first to Tweet this post)