Dall'esperimento del secchio di Newton agli Universi di Gödel |

Dall'esperimento del secchio di Newton agli Universi di Gödel

Marzo 26th, 2021 | by Marcello Colozzo |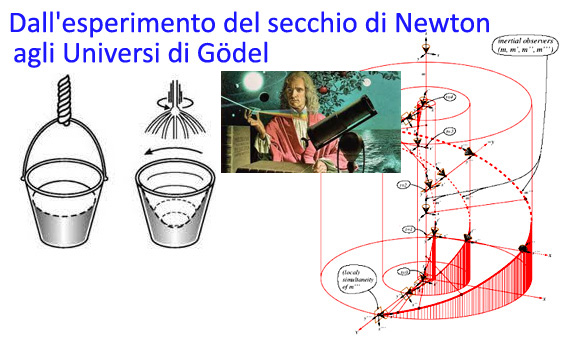

esperimento del secchio di Newton,universi di gödel,metrica di gödel

Come è noto, Newton utilizzò il famoso esperimento del secchio per dimostrare l'esistenza del cosiddetto spazio assoluto, quando invece la risposta più ovvia è: «l'acqua si muove rispetto al sistema di riferimento inerziale da cui si osserva il moto del secchio».

Dal momento che una trattazione matematica del moto di un fluido all'interno di un secchio che a sua volta ruota attorno a un asse verticale (asse di simmetria) è abbastanza complicata, consideriamo il seguente esperimento concettuale. Sia K0 un sistema di riferimento inerziale, rappresentato da una terna cartesiana Oxyz. Per una questione che apparirà chiara a breve, passiamo alle coordinate cilindriche

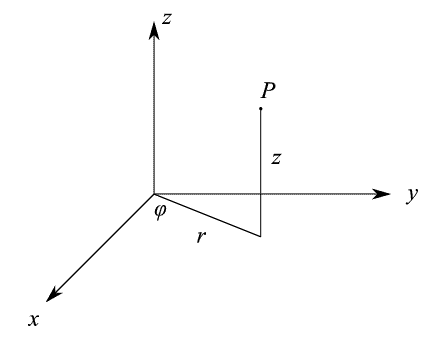
attraverso le note equazioni di trasformazione

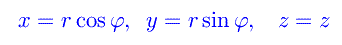
L'elemento di distanza, ovvero la distanza tra una coppia di punti infinitamente vicini (x,y,z),(x+dx,y+dy,z+dz), è

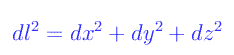
che può essere scritta in coordinate cilindriche (differenziando le equazioni di trasformazione):

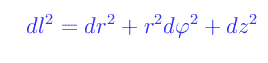
Supponiamo ora che tutti i punti dello spazio euclideo R³ riferiti a tale terna, ruotino nel senso che segue: preso ad arbitrio P(x₀,y₀,z₀) non appartenente all'asse z, P compie un moto circolare uniforme lungo una circonferenza contenuta nel piano z=z0, di centro (0,0,z₀) e di raggio r0. Una rappresentazione parametrica della traiettoria di P, utilizzando il tempo t misurato dall'orologio di K₀, è

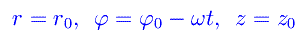
dove abbiamo utilizzato ovviamente le coordinate cilindriche in virtù della simmetria del problema. Si noti che la velocità angolare è -ω con ω > 0, cioè stiamo considerando una rotazione in senso orario (vista dall'osservatore inerziale con i piedi su O e la testa orientata nel verso dell'asse z). A breve sarà chiara la ragione della scelta del verso negativo. È estremamente istruttivo ricalcolare l'elemento di distanza relativo ai punti dello «spazio in uniforme rotazione». A tale scopo, lasciamo cadere il pedice 0 nelle coordinate di P, dopodiché non dobbiamo fare altro che sostituire il dφ con d(φ-ωt) per poi elevare al quadrato. Facendo i conti, esce:

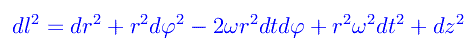
Chi mastica un pò di Relatività, avrà già pensato di passare dal 3-spazio x,y,z allo spaziotempo (ct,x,y,z) che nel caso di K₀ ha un elemento di «distanza»

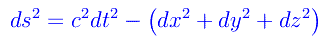
Abbiamo utilizzato le virgolette, poiché qui abbiamo un intervallo spaziotemporale ovvero la distanza tra due punti-eventi infinitamente vicini. Passando alle coordinate cilindriche nel 3-spazio

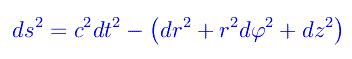
Il problema si complica se proviamo ad applicare il medesimo procedimento al 3-spazio in «uniforme rotazione». Infatti:

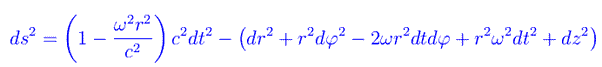
Come interpretare questo risultato? Da un punto di vista fisico, i punti del 3-spazio in «uniforme rotazione» compongono gli «elementi» (i.e. particelle) di un cosiddetto fluido di polvere (o di materia incoerente). Precisamente, per un fluido perfetto in equilibrio termodinamico, abbiamo un'equazione di stato

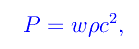
dove P,ρ sono rispettivamente pressione e densità, mentre w è un parametro adimensionale. Per w=0 otteniamo un'equazione di stato P=0 che descrive appunto, un fluido di materia incoerente. Nel formalismo della Relatività Generale, un fluido perfetto con equazione di stato scritta più sopra, ha un tensore energia-impulso

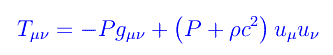
dove g_µν è il tensore metrico dello spaziotempo, mentre u_µ=g_µβu^β essendo /sub>u^β la 4-velocità dell'elemento di fluido. Nel caso in esame

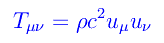
Ci siamo interessati a questa grandezza perché è il termine di sorgente delle equazioni di campo di Einstein (con costante cosmologica):

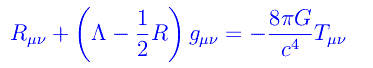
Non specifichiamo le altre grandezze. Ci limitiamo ad osservare che qui abbiamo un sistema di 10 equazioni differenziali alle derivate parziali, del secondo ordine nelle componenti del tensore metrico. Per un termine di sorgente dato dalla materia incoerente, Gödel trovò la soluzione:

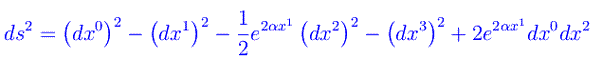
essendo α > 0 una costante con le dimensioni dell'inverso di una lunghezza. Si noti la somiglianza con il ds² trovato nel caso dello spazio rotante, a patto di utilizzare come coordinate del 3-spazio, le usuali coordinate cilindriche. Un calcolo più approfondito fornisce

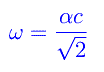
che conferma il legame tra i due casi. Nella soluzione di Gödel abbiamo, dunque, un fluido perfetto con equazione di stato P=0 il cui co-movimento (come si dice in RG) presenta una rotazione intrinseca. Allo stesso tempo, è chiaro che non esiste uno spazio di background (lo spazio assoluto di Newton) rispetto al quale definire una tale rotazione.

No TweetBacks yet. (Be the first to Tweet this post)