» Esercizi svolti di Matematica e Fisica

Curves in R³. Regular curve. Intrinsic triad. Osculating plane

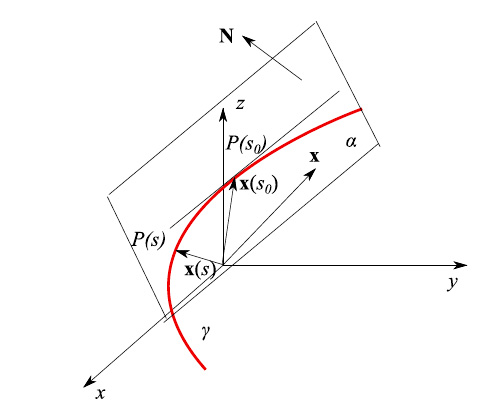
Le nozioni esposte nei numeri precedenti si gneralizzano facilmente alle curve in R³. Ad esempio, una rappresentazione parametrica di una curva gamma è una funzione vettoriale della variabile reale t (parametro della rappresentazione) definita in un intervallo (a,b).
Seguono le usuali definizioni di curva regolare e rappresentazione naturale. Nel caso tridimensionale, però, la curvatura k(s) non è sufficiente a determinare la curva, come succede nel caso bidimensionale. Ci serve una nuova grandezza nota come vettore unitario binormale che poi conduce alla definizione di piano osculatore.

Scarica la lezione in pdf

The notions expounded in the previous issues are easily understood in the curves in R³. For example, a parametric representation of a gamma curve is a vector function of the real variable t (parameter of the representation) defined in an interval (a, b).
The usual definitions of regular curve and natural representation follow. In the three-dimensional case, however, the curvature k (s) is not sufficient to determine the curve, as happens in the two-dimensional case. We need a new quantity known as the binormal unit vector which then leads to the definition of the osculating plane .

Download the lesson in pdf

Tags: Curves in R³, Regular curve. Intrinsic tria, sculating plane