Exercises in differential geometry
Dicembre 2nd, 2020 | by Marcello Colozzo |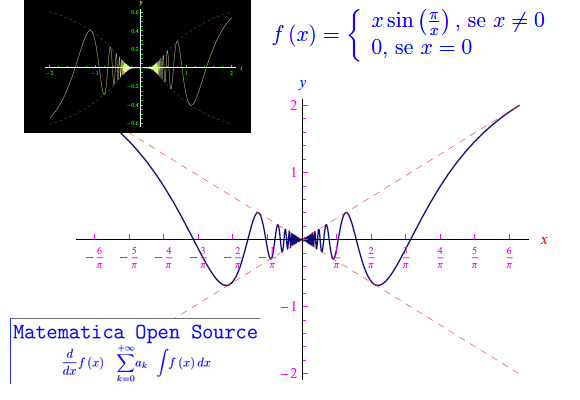
We propose a couple of differential geometry exercises, related to the study of curves in the plane . More precisely, we focus our attention on a class of curves which, although represented by functions of class C^oo (but not analytical!), have singular points. The first exercise concerns the presence of a cusp (or cusp ). The second exercise, on the other hand, is more dramatic: the direction of the tangent line is not defined in an assigned point, since the secant line swings indefinitely when we approach the singular point.
Downloaded the exercises in pdf
Proponiamo un paio di esercizi di geometria differenziale, relativi allo studio di curve nel piano. Più precisamente, focalizziamo la nostra attenzione su una classe di curve che pur rappresentate da funzioni di classe C^oo (ma non analatiche!) presentano punti singolari. Il primo esercizio riguarda la presenza di un punto cuspidale (o cuspide). Il secondo esercizio è, invece, più drammatico: la direzione della retta tangente non è definita in un assegnato punto, poiché la retta secante compie oscilla indefinitamente quando ci avviciaamo al punto singolare.
Tags: exercises in differential geometry, punto singolare, singular point
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











