Intepretazione formale dei punti di equilibrio (dinamica unidimensionale)
Novembre 16th, 2020 | by Marcello Colozzo |
Definizione
Dicesi punto di equilibrio del sistema di equazioni differenziali

un punto (ξ0,0) del piano delle fasi, tale che assegnata una condizione iniziale

il predetto sistema ammette l'unica soluzione

Osservazione
La lipchitzianità di F(x) è condizione sufficiente per l'unicità della suddetta soluzione.
Ciò premesso, dimostriamo il teorema:
Teorema
Assegnato il sistema di equazioni differenziali

con F(x) lipchitziana, il punto (ξ0,0) è di equilibrio se e solo se è un punto critico dell'energia.
Dim.
La condizione è sufficiente
Per ipotesi (ξ0,0) è punto di equilibrio. La lipchitzianità di F(x) implica che l'unica soluzione del sistema per una condizione iniziale x(t0)=ξ0,y(t0)=0 è
Dalla seconda equazione differenziale:
Cioè (ξ0,0) è punto critico.
La condizione è necessaria
Per ipotesi (ξ0,0) è un punto critico dell'energia, onde V'(ξ0)=0. Impostiamo il problema di Cauchy
Segue immediatamente che x(t)=ξ0,y(t)=0 è una soluzione di P. Dal momento che F(x) è lipchitziana, non esistono altre soluzioni, per cui (ξ0,0) è punto di equilibrio.
Corollario
Se (ξ0,0) è punto di equilibrio

Dim.
Segue immediatamente dalle equazioni del moto in forma integrale
Tags: moto unidimensionale, punti critici, punti di equilibrio
Articoli correlati
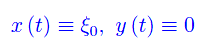
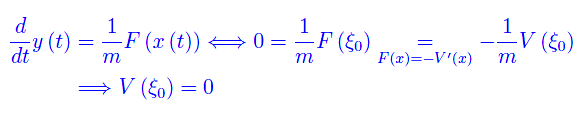
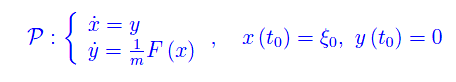


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











