Congetture di Aizerman e Kalman
Luglio 31st, 2020 | by Gianluca Angelone |
Congettura di Aizerman
Se il sistema lineare è asintoticamente stabile per ogni f(y)=ky, con k in [k1,k2] allora l'origine del sistema a ciclo chiuso, mostrato in Figura 1, con una non linearità tempo invariante
è asintoticamente stabile.
Aizerman congettura che se il vettore Ax+Bφ(y) è Hurwitz per ogni funzione lineare phi;(·), allora il punto x=0 può essere globalmente asintoticamente stabile per ogni funzione tale che il rapporto

Congettura di Kalman
Se il sistema lineare è asintoticamente stabile per ogni φ(y)=ky, essendo
allora l'origine del sistema a ciclo chiuso, mostrato in Figura 1, con una non linearità tempo invariante φ(·) tale che
è asintoticamente stabile.
Kalman congettura che se il vettore Ax+Bφ(y) è Hurwitz per ogni funzione lineare f(·), allora il punto x=0 può essere globalmente asintoticamente stabile per ogni f(·) continuamente differenziabile la cui pendenza rimane limitata in

Le due congetture sopra esposte possono essere viste come casi particolari di un problema più generale conosciuto nella letteratura di matematica applicata come Marcus-Yamabe Conjecture (MYC) [1] e, se fossero verificate, semplificherebbero molto l'analisi dei sistemi di controllo includenti non linearità. Purtroppo è stato dimostrato mediante controesempi [2] che queste congetture sono false. Occorre determinare altri criteri per ottenere condizioni sufficienti affinché il sistema di Figura 1 sia globalmente asintoticamente stabile.
Si noti che nella definizione di settore incrementale per σ1=0 si ottiene la definizione di settore utilizzata nella congettura di Aizerman, mentre per σ2->σ1 si ottiene il settore relativo alla congettura di Kalman.
Tags: congettura di Aizerman, congettura di Kalman, Marcus-Yamabe Conjecture
Articoli correlati

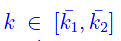



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











