Puleggia ideale

Giugno 18th, 2020 | by Marcello Colozzo |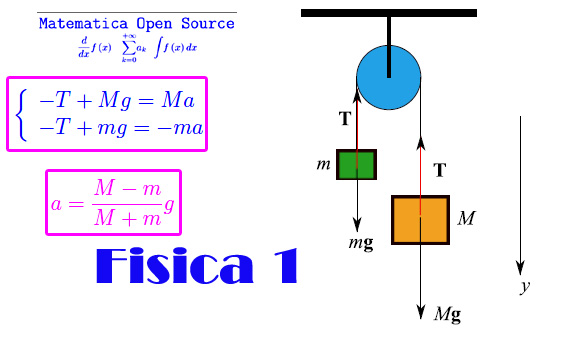

Il sistema meccanico di fig.1 è costituito da una puleggia ideale, cioè un disco di massa trascurabile nel cui solco ("gola" della puleggia) passa una fune ideale (i.e. inestensibile e di massa trascurabile). L'idealità della puleggia implica una rotazione del disco (fig. 1) senza attrito.
A) Studiare il moto delle due masse M,m con M>m. B) Studiare il caso limite M >> m. C) Cosa succede se M=m?

Soluzione
Dopo aver orientato un asse verticale y verso il basso come in fig. 1, applichiamo il secondo principio della dinamica al blocco di massa M:

Dal momento che non conosciamo T, abbiamo bisogno di una seconda equazione, che è l'equazione del moto del blocco di massa m. Osserviamo preliminarmente:

fune di massa trascurabile => la tensione trasmessa è costante lungo la fune medesima;
fune inestensibile => i due blocchi si muovono con accelerazioni aventi lo stesso modulo.

Ne consegue l'equazione del moto per il blocco m

Abbiamo così ottenuto il sistema di equazioni lineari

Sottraendo membro a membro

da cui ricaviamo il modulo dell'accelerazione

Conclusione quesito A: entrambi i blocchi si muovono verticalmente con accelerazione di modulo (eq. scritta sopra); il blocco M verso il basso, il blocco m verso l'alto.

Quesito B

Cioè M è approssimativamente in caduta libera.
Quesito C

ovvero il sistema meccanico è in equilibrio dinamico. In particolare, se i blocchi sono inizialmente fermi, il sistema perservera nello stato di quiete.

Indice delle lezioni/esercizi

No TweetBacks yet. (Be the first to Tweet this post)