Momento statico di una figura piana, rispetto all'asse y

Maggio 29th, 2020 | by Marcello Colozzo |

momento statico,figura piana,flaccavento,integrali doppi
Fig. 1


Esercizio n.6, pag. 234 del Flaccavento

Calcolare il momento statico rispetto all'asse y della figura limitata dal primo quadrante, da y=x² e dalla semicirconferenza che ha centro nel punto (1,0) e raggio 1.

Soluzione
L'equazione della circonferenza di centro (1,0) e raggio 1 è ovviamente


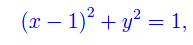
da cui ricaviamo l'equazione della semicirconferenza giacente nel semipiano y=0:

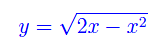
Abbiamo quindi il dominio normale rispetto all'asse x


come illustrato in fig. 1. Il momento statico rispetto all'asse y è dato da


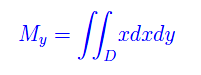
Applicando le formule di riduzione degli integrali doppi


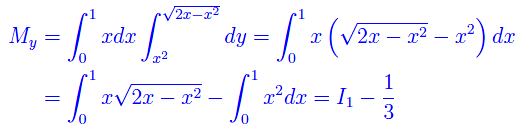
Calcoliamo a parte


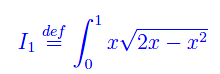
Osserviamo che


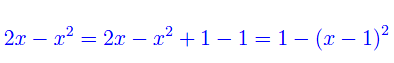
Tale sviluppo suggerisce la sostituzione

Vediamo come cambiano gli estremi di integrazione


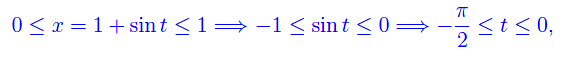
onde

Sostituendo nell'equazione scritta più sopra, otteniamo

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio