Per Mathematica può essere una polinomiale di grado variabile da 1 a 7

Aprile 20th, 2020 | by Marcello Colozzo |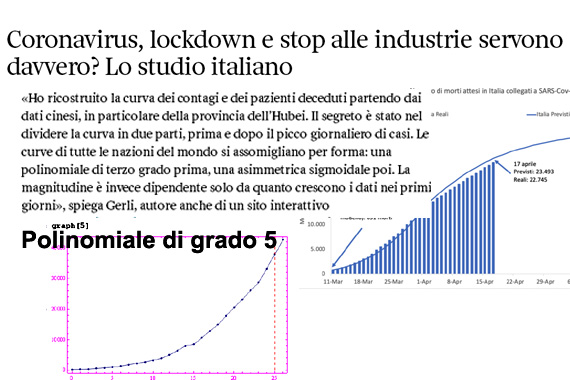

C'è un interessante articolo de Il Corriere che riporta uno studio italiano su gli effetti reali del lockdown nella pandemia da coronavirus. Nello specifico, sembrano determinanti solo i primi 17 giorni di quarantena. Il modello matematico proposto sembra basato su una coppia di equazioni differenziali, di cui una prima dovrebbe restituire una funzione non elementarmente esprimibile, ma comunque interpolabile numericamente attraverso una polinomiale di terzo grado. La seconda, invece, restituisce come soluzione una sigmoidale asimmetrica. Le predette soluzioni vanno raccordate nell'istante del raggiungimento del picco massimo dei contagi giornalieri, corrispondente al punto di flesso della funzione che enumera gli "attualmente positivi".
Per curiosità, abbiamo provato a plottare i primi 26 dati forniti dal sito web della protezione civile relativi agli "attualmente positivi". L'interpolazione numerica eseguita nell'ambiente di calcolo Mathematica non sembra fornire alcuna prova al riguardo del grado 3 del polinomio interpolante. Per essere più precisi, si ottiene una buona interpolazione per n (grado del polinomio) variabile da 1 a 7. Per i dettagli, scarica il codice Mathematica in pdf

No TweetBacks yet. (Be the first to Tweet this post)