Non può essere una polinomiale di grado inferiore a 6
Aprile 20th, 2020 | by Marcello Colozzo |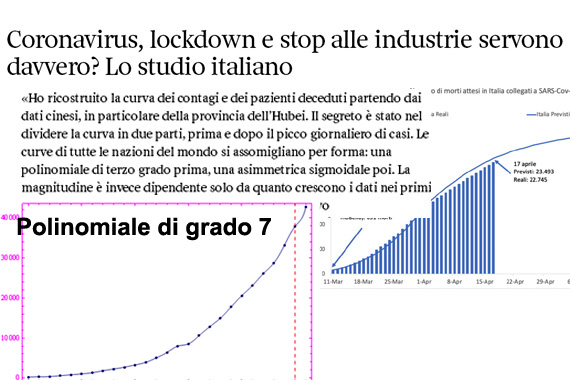
Aggiornamento del post precedente.
Per quanto precede, il software Mathematica nell'eseguire una interpolazione, restituisce una cosiddetta "polinomiale", il cui grado può essere settato all'interno dell'istruzione Interpolation. È chiaro che i coefficienti del polinomio interpolante cambiano passando da un dato discreto all'altro. Ad esempio, se il grado è n=1, otteniamo una spezzata ovvero una funzione lineare a tratti. Ciò perché, Mathematica calcola il coefficiente angolare della retta che unisce una coppia di dati discreti. La possibilità di tale approssimazione deriva sostanzialmente dal fatto che pur non essendo la funzione degli "attualmente positivi" non elementarmente esprimibile, è comunque una funzione analitica, ossia approssimabile da una serie di Taylor punto per punto. Ed è chiaro che troncando la serie otteniamo un polinomio di grado assegnato.
Tuttavia, eseguendo le simulazioni non è difficile rendersi conto che il minimo grado è 6, poiché polinomi di grado minore non riproducono il punto di flesso.
Tags: coronavirus, picco massimo, polinomiale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











