Coronavirus: non c'è mai stata una crescita esponenziale

Marzo 28th, 2020 | by Marcello Colozzo |

coronavirus,crescita esponenziale,equazioni differenziali,integrazione numerica — **Fig. 1**

Il nostro punto di partenza è una popolazione a tre componenti:

Attualmente positivi.
Guariti.
Deceduti.

Se A(t),G(t) e D(t) sono le funzioni che conteggiano gli individui di singola componente, si ha che il numero di contagiati totali al tempo t, è dato da:

Assumiamo che N(t) sia l'unica soluzione del seguente problema di Cauchy

essendo t₀=0d =24/02/2020, mentre 0 < λ <= 1 è un parametro da definire computazionalmente. Nel paradigma dei sistemi dinamici, l'equazione differenziale appena scritta definisce un sistema non autonomo, in quanto la funzione f(t,N)=a(t)N^λ a secondo membro dipende esplicitamente dal tempo. Inoltre, la maggior parte dei modelli di crescita di una popolazione prevedono una proporzionalità tra la velocità di diffusione N ed dN/dt. Incidentalmente nel caso speciale α(t)=C, =1, λ si ha la crescita esponenziale:

si ha una crescita esponenziale. Nel caso generale non conosciamo la funzione α(t) se non attraverso i dati giornalieri forniti dal sito web della Protezione civile. Per poter inserire questi dati in un'equazione differenziale del tipo visto sopra, dobbiamo necessariamente eseguire un campionamento della variabile t con ampiezza di campionamento pari a 1 d , in modo da poter scrivere:

Per quanto precede, i dati N_k,N_k+1 sono forniti dal sito della Protezione civile, per cui possiamo calcolare giornalmente

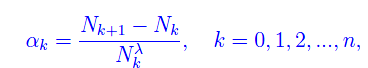
dove l'intero naturale n identifica l'istante giornaliero t_n. Ad esempio, in data odierna (28/03, i dati sono aggiornati al giorno precedente) abbiamo l'andamento graficato in fig. (assumendo λ=0.1)

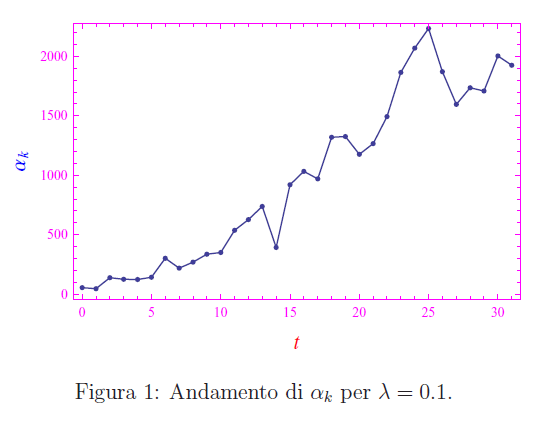
Eseguendo un'interpolazione con Mathematica, otteniamo una funzione α_int(t) il cui grafico è riportato in fig.

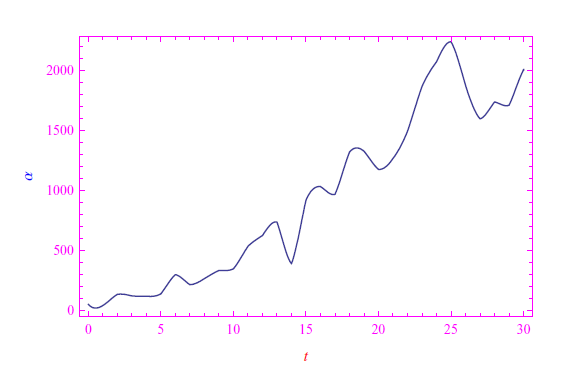
mentre in figura confrontiamo i due andamenti (discreto e continuo (per interpolazione))

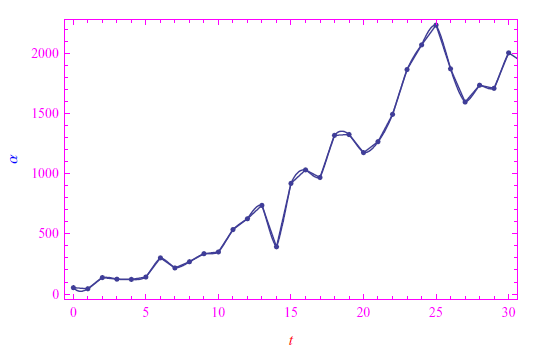
Una volta ottenuta la funzione α_int(t) possiamo integrare per quadrature l'equazione differenziale scritta all'inizio. Tuttavia, per evitare problemi derivanti dal calcolo di un integrale definito di una funzione ottenuta per interpolazione, preferiamo chiedere a Mathematica di integrare numericamente la predetta equazione. In fig. 1 (top della pagina) iportiamo l'andamento della soluzione numerica confrontata con l'andamento reale della diffusione virale.

No TweetBacks yet. (Be the first to Tweet this post)