Coronavirus. La logistica dei decessi

Marzo 17th, 2020 | by Marcello Colozzo |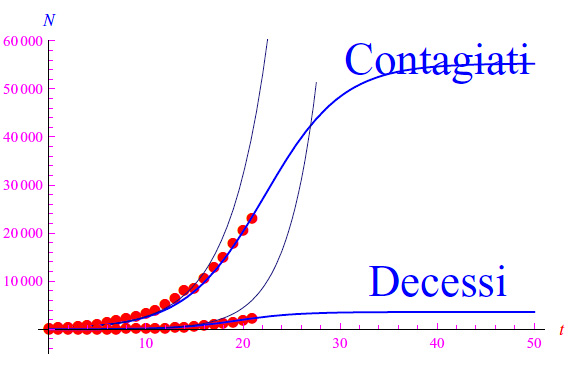

coronavirus,decessi, logistica,equazione differenziale
Fig. 1


Con i dati aggiornati, vediamo che il coefficiente α ha subito un'ulteriore riduzione. Abbiamo poi plottato i dati delle persone decedute, approssimando poi con la seguente logistica:


dove: M0 è il numero iniziale di deceduti, <αd> è la media del parametro αd computato con i predetti dati. Il coefficiente γ serve per "smorzare" l'esponenziale. Dati numerici ottenuti:

Il grafico è in fig. 1.

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio