[Calcolo tensoriale] Contrazione

Marzo 10th, 2020 | by Marcello Colozzo |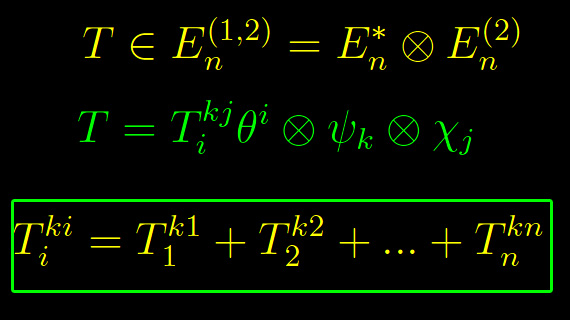

Spesso i tensori vengono definiti attraverso il Criterio di tensorialità, vale a dire mediante una legge di trasformazione quando si passa da una base all'altra. Tale definizione non ha però un carattere intrinseco, per cui è preferibile definirli come applicazioni multilineari. Tuttavia, in molte operazioni è più facile riferirsi esclusivamente alle componenti in una base assegnata. Iniziamo a definire

Definizione
Dicesi operazione di contrazione la saturazione di un indice covariante e di un indice controvariante.

Ad esempio, consideriamo un tensore misto di rango 2:

per cui se

è una base di E_n^(1,1), si ha:

essendo T_i^k le n² componenti di T nella predetta base. Eseguendo la contrazione dell'indice covariante i e dell'indice controvariante k:

che è manifestamente uno scalare, che chiamiamo traccia del tensore T. Consideriamo ora un tensore misto di rango 3, precisamente 1-covariante e 2-controvariante:

per cui se

è una base di E_n^(1,2), si ha

dove le T_i^kj sono le n³ componenti di T nella predetta base. Eseguendo la contrazione dell'indice covariante i e dell'indice controvariante j:

Applicando il criterio di tensorialità vediamo che le T_i^ki sono le n componenti di un tensore controvariante di rango 1, ossia di un vettore di E_n. Da ciò segue che l'operazione di contrazione abbassa di 2 unità il rango di un tensore. Infatti, nel primo esempio siamo passati da un tensore misto di rango 2 a uno scalare (traccia del tensore), mentre nel secondo esempio la contrazione di un tensore di rango 3 ha restituito un tensore di rango 1.

A questo punto è immediato generalizzare considerando un tensore misto r-covariante e s-controvariante: