[¯|¯] Tensori controvarianti di rango r (parte seconda)
Marzo 6th, 2020 | by Marcello Colozzo |
Nel numero precedente abbiamo definito le "componenti" di un tensore controvariante di rango r. È chiaro che tale locuzione ha senso solo se è stata assegnato innanzitutto uno spazio vettoriale di appartenenza, e poi una sua base. A tale scopo definiamo innanzitutto l'insieme delle applicazioni r-lineari introdotte nel numero precedente:
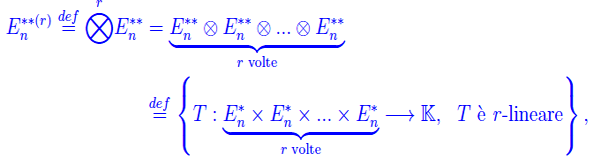
dove il doppio asterisco denota lo spazio biduale di En. Siccome esiste un isomorfismo naturale tra un qualunque spazio vettoriale e il suo biduale, possiamo identificare En** con En, per cui scriviamo semplicemente:

avendo però l'accortezza di denotare una base di En con un simbolo del tipo

per ricordare che stiamo in realtà lavorando sullo spazio biduale. Più precisamente, se {ei} è una base assegnata di En, si ha che la base duale ad essa associata è
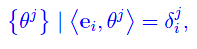
mentre la base biduale associata alla base {ei} ovvero la base duale associata a {θj}, è
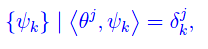
che è ovviamente una base En, tuttavia in generale distinta dalla base di partenza {ei}.
Riepilogando: lavoriamo su Enr assumendo come base il sistema {ψk}}. Introducendo in Enr le usuali leggi di composizione, si ha che tale spazio assume la struttura di spazio vettoriale su K .
Definizione
Lo spazio vettoriale Enr si dice spazio prodotto tensoriale r volte di En
Teorema
Il sistema
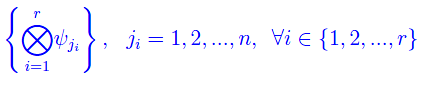
è una base di Enr
Dim.
Dobbiamo dimostrare che si stratta di un sistema linearmente indipendente di ordine massimo. Comunque prendiamo una r-pla di 1-forme (elementi di En*), dovrà essere per definizione di prodotto tensoriale
cioè
Scriviamo (con ovvio significato dei simboli):
Tenendo conto della relazione scritta più sopra
Se in particolare, prendiamo i vettori di base:
onde la precedente diviene:
Ne consegue che il sistema
è lineramente indipendente. Proviamo ora che si tratta di un sistema di ordine massimo. Tenendo conto delle relazioni scritte più sopra:
per cui il sistema
è linearmente dipendente, onde l'asserto.
Dal teorema appena dimostrato si ha:


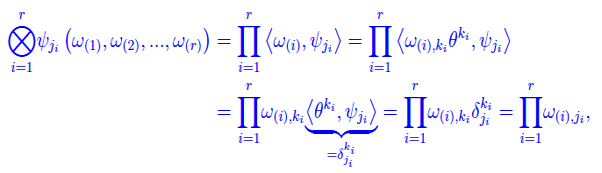


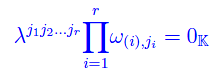







 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











