[¯|¯] Pendolo parabolico di ordine n
Febbraio 29th, 2020 | by Marcello Colozzo |
Esercizio (Pendolo parabolico di ordine n)
Una pallina di massa m è lasciata cadere lungo una guida disposta in un piano verticale, avente la forma di una parabola di ordine n, cioè y=αxn, dove α > 0 e n è un intero naturale pari. Studiare il moto della pallina, trascurando l'attrito e la resistenza dell'aria.
Soluzione
L'equazione della guida suggerisce l'esistenza di un sistema di coordinate la cui origine è il vertice della parabola. Per ipotesi la pallina è lasciata cadere da una altezza y0, per cui la sua energia meccanica iniziale è puramente potenziale:
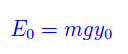
Di contro, l'energia meccanica a tutti i tempi è
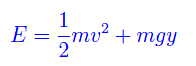
Trascurare l'attrito e la resistenza dell'aria equivale ad assumere la conservazione dell'energia meccanica:
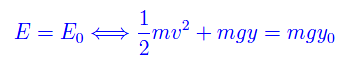
Cioè
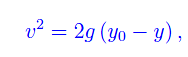
da cui vediamo che la pallina non potrà superare la quota iniziale. È facile convincersi che i moti componenti lungo gli assi coordinati sono periodici. In particolare, il moto lungo l'asse x avviene tra -x0 e +x0, dove
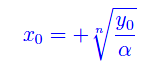
Segue
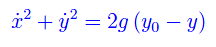
Ma
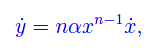
per cui
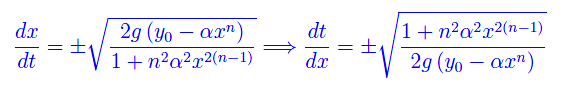
Il periodo del moto è
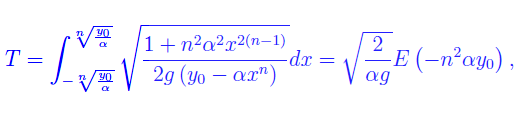
essendo
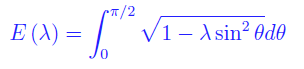



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











