[¯|¯] Differenziale di una funzione vettoriale. Matrice jacobiana
Febbraio 8th, 2020 | by Marcello Colozzo |
Premettiamo alcuni richiami di Analisi matematica 1 e Analisi matematica 2.
Sia f:X->R reale di una variabile reale, derivabile in X. La funzione lineare omogenea dell'incremento Δx, data da

si dice differenziale di f. Se applichiamo tale definizione alla funzione identica f(x)=x, si ottiene dx=Δx per cui il differenziale può essere scritto come:

Teorema
Nelle ipotesi precedenti, se Δf è l'incremento della funzione corrispondente all'incremento Δx della variabile indipendente, si ha:
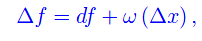
dove ω(Δx) è, per Δx->0, un infinitesimo di ordine superiore a Δx.
Ora consideriamo il caso di una funzione reale di n variabili reali:
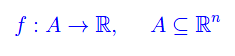
Se f è dotata in A di derivate parziali
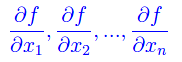
si dice differenziale totale di f la seguente funzione lineare degli incrementi Δx1,...,Δxn delle variabili indipendenti:
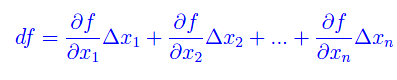
Anche in questo caso è facile mostrare che
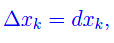
onde
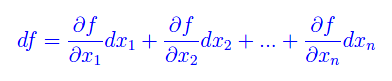
Sussiste il teorema:
Teorema
Se è di classe C^1 su A, si ha:
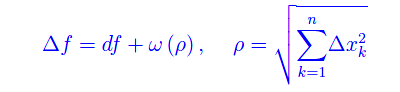
dove ω(ρ) è, per ρ->0, un infinitesimo di ordine superiore rispetto a ρ.
Ciò premesso, ci proponiamo di generalizzare la nozione di differenziale totale a una funzione vettoriale di variabile vettoriale:
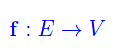
dove E e V sono i soliti spazi vettoriali su un campo K, supponendo di aver assegnato le rispettive basi:
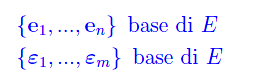
Abbiamo che f(x) è un vettore a m componenti:
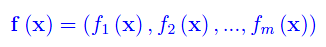
Il differenziale totale della k-esima componente è
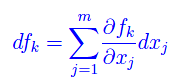
Definizione
Dicesi differenziale della funzione vettoriale f(x), il vettore
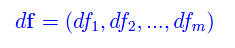
Il vettore le cui componenti (nella base {e1,...,en) sono i differenziali delle componenti di x, è
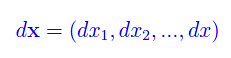
Inoltre
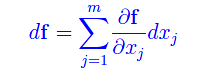
rammentando che
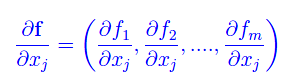
Quindi il differenziale df è una funzione vettoriale lineare della variabile vettoriale dx, e come tale è dotata di una matrice rappresentativa rispetto alle basi assegnate. Per esplicitare gli elementi di matrice, scriviamo per esteso i differenziali delle componenti:
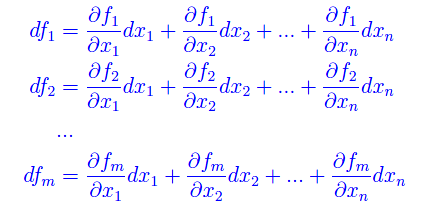
Per definizione di matrice rappresentativa, si ha:
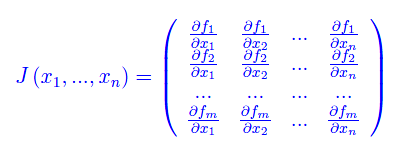
che si chiama matrice jacobiana della funzione vettoriale f(x) rispetto alle predette basi. Se i due spazi vettoriali hanno la stessa dimensione n, la matrice jacobiana è quadrata di ordine n, e il suo determinante si dice jacobiano della funzione, e si indica con
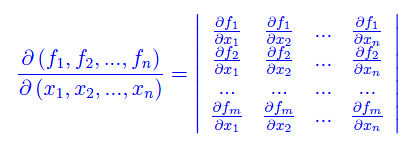
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











