[¯|¯] Moto rettilineo uniforme

Dicembre 13th, 2019 | by Marcello Colozzo |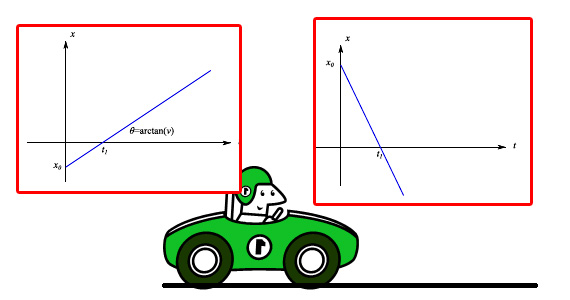

Nel caso particolare di un'equazione oraria lineare:

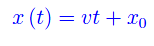
con v e x₀ costanti assegnate, si ha:

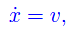
cioè la velocità scalare istantanea è costante. In termini di rapporto incrementale, risulta evidente:

In altri termini, la velocità scalare istantanea coincide con la velocità scalare, e il moto si dice rettilineo uniforme velocità istantanea e la velocità media sono identicamente coincidenti. Il diagramma orario è manfestamente la retta del piano cartesiano tx di coefficiente angolare v e ordinata all'origine x₀, ove quest'ultimo parametro è la coordinata iniziale del punto materiale. Nella fig. 1 in alto a sinistra è riportato il diagramma orario del moto di un punto materiale che si muove lungo l'asse x. Il moto è rettilineo uniforme con velocità v (coefficiente angolare della retta). Il verso è quello delle x crescenti. All'istante iniziale t=0 il punto occupa la posizione iniziale di ascissa x₀ < 0, mentre nell'istante t₁=-x₀/v transita per l'origine , proseguendo verso +oo.

Nella stessa figura, in alto a destra troviamo il diagramma orario del moto di un punto materiale che si muove lungo l'asse x. Il moto è rettilineo uniforme con velocità v. Il verso è quello delle x decrescenti. All'istante iniziale t=0 il punto occupa la posizione iniziale di ascissa x₀ > 0, mentre nell'istante t₁=x₀/v transita per l'origine, proseguendo verso -oo.
Ne consegue che nel primo caso la velocità vettoriale è

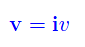
mentre nel secondo

In entrambi i casi si tratta di un vettore costante.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Indice delle lezioni

No TweetBacks yet. (Be the first to Tweet this post)