[¯|¯] Integrale di un vettore

Dicembre 10th, 2019 | by Marcello Colozzo |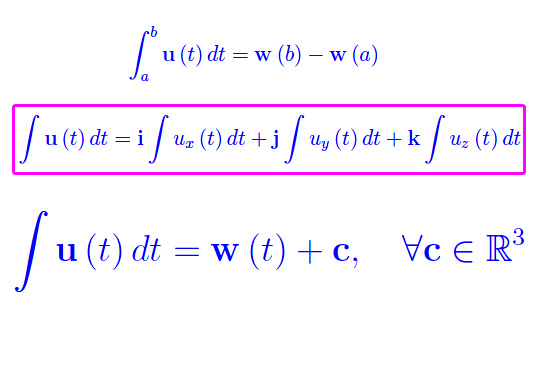

Nel numero precedente abbiamo definito l'operazione di derivazione di un vettore:

Come è noto, nel caso di funzioni scalari l'inversione della (eq:der) definisce l'operazione di integrazione. Per una funzione vettoriale, tale operazione consiste nel determinare una primitiva di un'assegnata funzione vettoriale:

Definizione
Chiamiamo il seguente oggetto:

integrale indefinito della funzione vettoriale u(t).

Una primitiva è definita a meno di una costante (vettoriale) additiva. Cioè se w(t) è una assegnata primitiva di u(t), si ha:

Segue la rappresentazione cartesiana

dove u_x(t),u_y(t),u_z(t) sono le componenti cartesiane del vettore u(t).
Definizione
Se u(t) è continua in [t₁,t₂], comunque prendiamo a,b nel predetto intervallo:

è l'integrale definito della funzione vettoriale u(t) esteso da a a b.

Se w(t) è una qualunque primitiva di u(t), sussiste la formula fondamentale del calcolo integrale: