[¯|¯] Campo elettrico determinato da una piano uniformemente carico

Novembre 1st, 2019 | by Marcello Colozzo |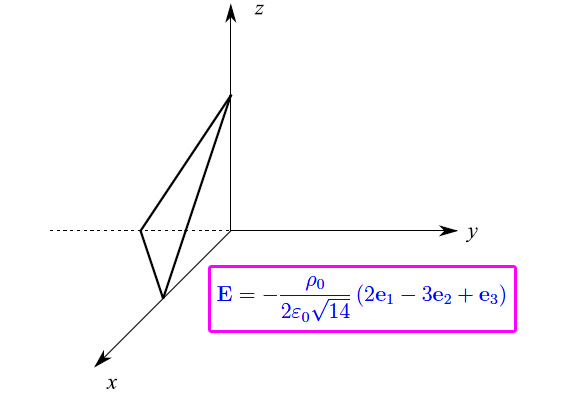

campo elettrico,piano uniformemente carico — **Fig. 1**

Esercizio
Un piano uniformemente carico ha equazione:

dove i coefficienti sono espressi in metri. Determinare il campo elettrico nel semispazio contenente l'origine.

Soluzione
Da un esercizio precedente sappiamo che

dove n è uno dei versori ortogonali al piano assegnato (si sceglie uno dei due versori a seconda del semispazio considerato). Come è noto dalla Geometria analitica, un vettore ortogonale al piano ax+by+cz+d=0 è

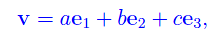
onde

Nel caso in esame

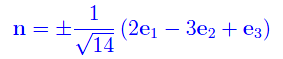
Per rimuovere l'ambiguità del segno, determiniamo i punti di intersezione del piano con gli assi coordinati, come illustrato in fig. 1. Da qui vediamo che dobbiamo prendere il segno inferiore, da cui il risultato illustrato nella predetta figura.

No TweetBacks yet. (Be the first to Tweet this post)