» Esercizi svolti di Matematica e Fisica

[¯|¯] Ipotesi di Riemann e Brown Noise

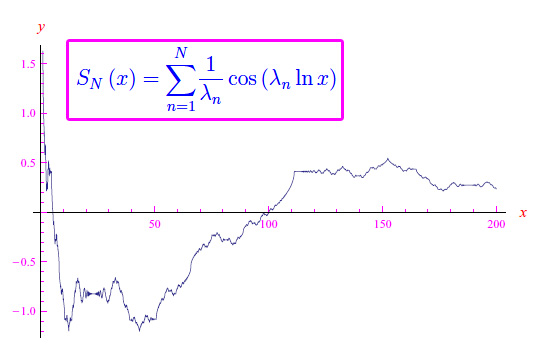
Nello sviluppo in serie della funzione di distribuzione dei primi π₀(x) trovato da Riemann nel 1856, compare una serie in cui la convergenza è modulata da una infinità numerabile di parametri (zeri non banali della funzione zeta di Riemann). Siamo dunque in presenza di una serie atipica, nel senso che la variabile indipendente x del termine n-esimo è svincolata dall'indice di somma. Un altro aspetto interessante è la presenza della funzione coseno con argomento contenente i predetti parametri, e con dipendenza logaritmica dalla variabile reale x.

Simulando con Mathematica una serie di questo tipo, si giunge a un comportamento del tipo Brown Noise per ciò che riguarda una assegnata somma parziale.

Per i dettagli, scarica il file pdf

Tags: brown noise, ipotesi di Riemann, Serie di funzioni