[¯|¯] La densità degli zeri della zeta di Riemann e il teorema della divergenza

Settembre 7th, 2019 | by Marcello Colozzo |

congettura di riemann,densità degli zeri, teorema della divergenza

Se g_N è un qualunque numero di Gram della funzione di Riemann-Siegel, dopo un tot di conti (utilizzando l'indicatore logaritmico della funzione ? di Riemann), procedendo per assurdo abbiamo ricavato questa formula:

a cui possiamo tranquillamente applicare il ben noto teorema della divergenza (in 2 dimensioni). Vediamo le singole grandezze: µ(x,y) è la densità degli zeri non banali nel dominio rettangolare

Si sceglie un punto di Gram in modo da non avere zeri sulla frontiera di tale dominio. La densità è ovviamente deltiforme:

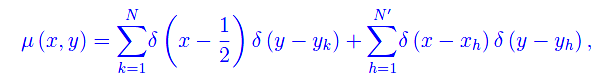
essendo N' il numero di zeri non banali che non cadono sulla linea critica. Si osservi che - procedendo per assurdo - non si può porre N'=1, giacché per le ben note proprietà di simmetria della ξ, uno zero fuori della linea critica, determina univocamente altri 3 zeri.

No TweetBacks yet. (Be the first to Tweet this post)