[¯|¯] Prodotti infiniti

Agosto 30th, 2019 | by Marcello Colozzo |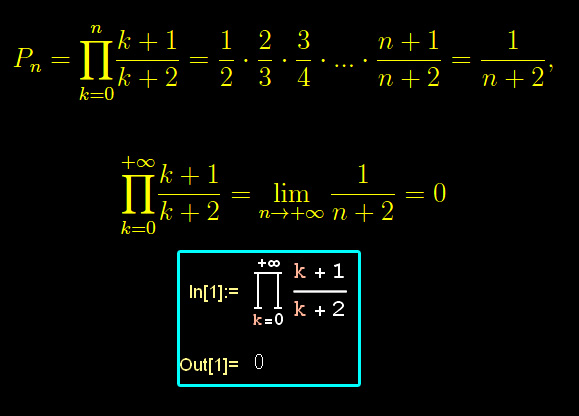

Definizione
Assegnata una successione di numeri complessi

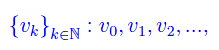
si dice prodotto infinito (numerico) relativo a tale successione, il simbolo:

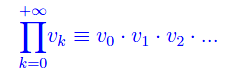
I termini della successione si dicono fattori del prodotto infinito assegnato.
Si dice prodotto parziale di ordine n il numero complesso:

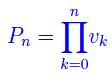
Al prodotto infinito assegnato possiamo, dunque, associare univocomanete la successione di numeri complessi:

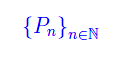
Definizione
Il prodotto infinito

è convergente se

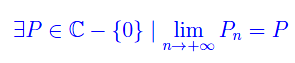
In altri termini, un prodotto infinito è convergente se tale è la successione dei prodotti parziali; in particolare tale successione tende a un limite non nullo. In tal caso, il predetto limite si chiama valore del prodotto infinito, e si scrive:

Definizione
Il prodotto infinito

è nullo se se la successione dei prodotti parziali è infinitesima. In tal caso scriviamo

Evidentemente

Cioè se è nullo uno dei fattori, il prodotto infinito è nullo. Ma non è vero il viceversa. Inoltre:

Cioè se la successione dei fattori è infinitesima, il prodotto infinito è nullo. Ma non è vero il viceversa. Quest'ultimo punto non è così ovvio. Prendiamo allora il prodotto infinito sui reali (la generalizzazione a C è immediata)