[¯|¯] La funzione xi di Riemann e gli spin networks di Penrose
Agosto 28th, 2019 | by Marcello Colozzo |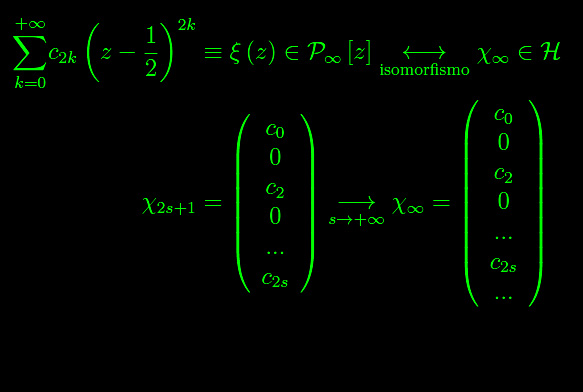
Riprendiamo lo sviluppo di Taylor della funzione ξ(z) di Riemann, ma questa volta di punto iniziale z=1/2 anzichè z=0. Le ragioni di questa modifica sono da ricercarsi nel fatto che è già noto l'ultimo sviluppo, come possiamo leggere da quest'articolo. Nella nostra notazione abbiamo:

In particolare abbiamo uno sviluppo con termini pari, a causa della simmetria della ξ(z) rispetto alla retta per il punto del piano complesso z=1/2 e parallela all'asse immaginario. Osserviamo che il predetto sviluppo venne elaborato da Riemann, il quale fornì per i coefficienti la seguente espressione:

essendo θ(t) la funzione theta di Jacobi:
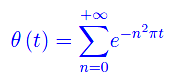
La somma parziale di ordine n è il polinomio di grado 2n
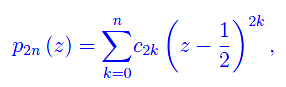
ed è un elemento dello spazio vettoriale complesso P2n[z] i cui elementi sono i polinomi di grado minore o uguale a 2n. Come è noto, tale spazio dimensione 2n+1, ed è isomorfo a C2n+1. Interpretando l'intero naturale n alla stregua di un numero quantico di spin (s) e introducendo in C2s+1 una struttura di spazio unitario (definendo un prodotto hermitiano e relativi assiomi), si ha che il predetto spazio implementa gli stati di spin per una particella di spin s in regime non relativistico. Più precisamente:
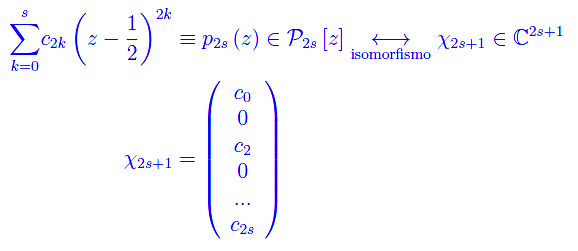
Per s?+8, lo spazio unitario C2s+1 diviene uno spazio di Hilbert (in quanto infinito-dimensionale):
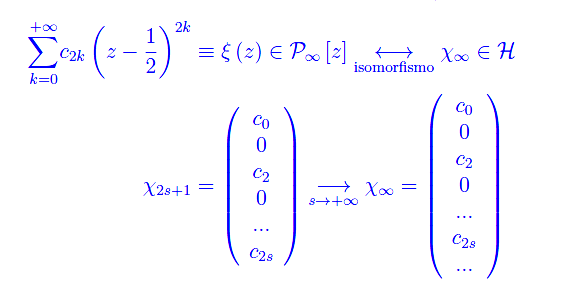
Come è noto, tali oggetti hanno un significato fisico solo se sono normalizzabili (in tal caso di parla di funzioni d'onda di spin o spinori). A tale scopo, osserviamo che una qualunque trascendente intera (e quindi, la funzione ξ(z)) è definita dalla distribuzione dei suoi infiniti zeri ρk, a meno di un coefficiente di proporzionalità. In altri termini, la successione {ρk} individua un sottospazio vettoriale 1-dim. di H. Ne consegue che possiamo considerare non una ma oo¹ funzioni &xi(z) che hanno in comune gli zeri. Tra queste infinite funzioni, esiste ed è unica quella di norma unitaria. Dalla definizione di norma:

per cui possiamo normalizzare lo spinore:
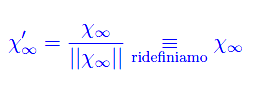
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











