[¯|¯] Esercizio sugli spazi vettoriali euclidei

Maggio 31st, 2019 | by Marcello Colozzo |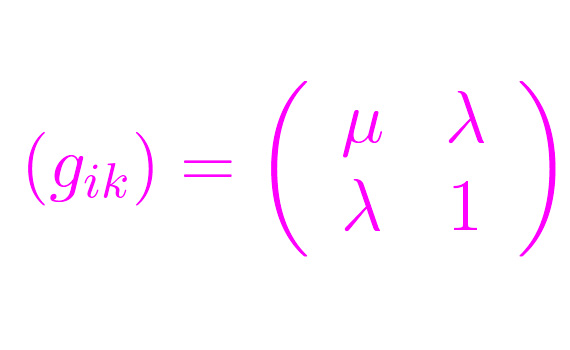

spazio euclideo,spazio pseudoeuclideo,metrica — **Fig. 1**

Esercizio
Assegnata una base {e_i} di uno spazio vettoriale euclideo 2-dimensionale, il cui tensore metrico ha la matrice rappresentativa nella predetta base, riportata in fig. 1, determinare per quali valori di λ e µ, tale spazio risulta propriamente euclideo.

Soluzione
Abbiamo

Segue

Se μ<=0

Quindi deve essere µ>0, per cui

Se invece

lo spazio è pseudoeuclideo. Per µ=0, un qualunque λ≠0 determina uno spazio pseudoeuclideo. Non può essere µ=λ=0, poiché in tal caso la metrica è degenere. Infine, per g < 0 un qualunque valore reale di λ determina uno spazio pseudoeuclideo.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.