[¯|¯] Criterio 1 di sommabilità (utile per gli esercizi)
Febbraio 23rd, 2019 | by Marcello Colozzo |
Per lo svolgimento degli esercizi sono utili altri criteri (sufficienti). Vediamo il n. 1 in cui consideriamo una funzione reale f della variabile reale x e un intervallo limitato [a,b].
Criterio 1
Sia f continua in [a,b]-{x0}, con x0 punto di discontinuità di seconda specie

Dim.
Poniamo
Da questo esempio
da cui l'asserto 1 in virtù del criterio 2 del n. precedente. La parte 2 si dimostra in maniera analoga.
Esempio
Consideriamo la funzione

nell'intervallo (0,1]. Il punto x=0 è di discontinuità di seconda specie, giacché la funzione non ammette limite per x->0. D'altra parte

da cui la sommabilità di f nel predetto intervallo. In fig. 1 è graficata la funzione assegnata. Vediamo che il grafico è un'oscillazione sinusoidale modulata dalle curve y=±x^(1/2), per cui in ogni intorno destro di x=0 la funzione compie infinite oscillazioni di ampiezza divergente per x->0. Tuttavia, l'area del rettangoloide generalizzato è finita. Precisamente, l'integrale si esprime attravero la funzione integrale di Fresnel

trovando

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.


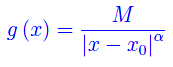
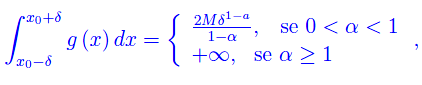



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









