[¯|¯] Funzioni integrabili e funzioni sommabili
Febbraio 15th, 2019 | by Marcello Colozzo |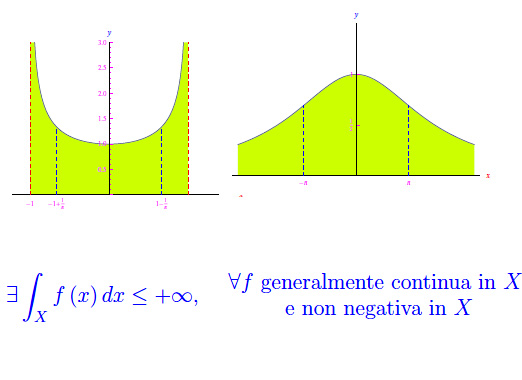
Alcuni esempi numerici esaminati nei numeri precedenti, impongono le seguenti definizioni:
Definizione
Una funzione generalmente continua in un intervallo X (limitato o illimitato) si dice integrabile , se comunque prendiamo una successione di domini {Tn} tali che
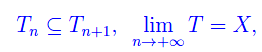
è univocamente determinato il limite:
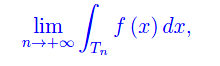
che è l'integrale generalizzato di f esteso all'intervallo X, ossia
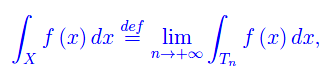
risultando
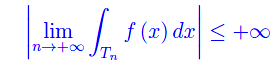
Nota. Nel caso particolare di una funzione non negativa, si ha ovviamente
Nel caso particolare
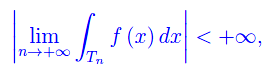
la funzione si dice sommabile.
Osservazione
Per determinazione univoca intendiamo che il limite
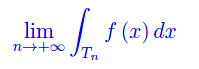
è indipendente dalla successione {Tn}. Cioè, se prendiamo due successioni distinte
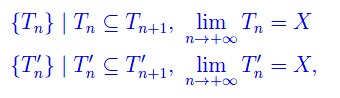
si ha
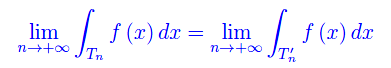
Per quanto visto negli esempi dei post precedenti, le funzioni generalmente continue e non negative in X (limitato o illimitato) sono comunque integrabili.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: funzioni integrabili, Funzioni sommabili, integrabilità, sommabilità
Articoli correlati
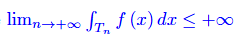



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









