[¯|¯] Integrali curvilinei dal Flaccavento (lavoro di una forza)

Gennaio 2nd, 2019 | by Marcello Colozzo |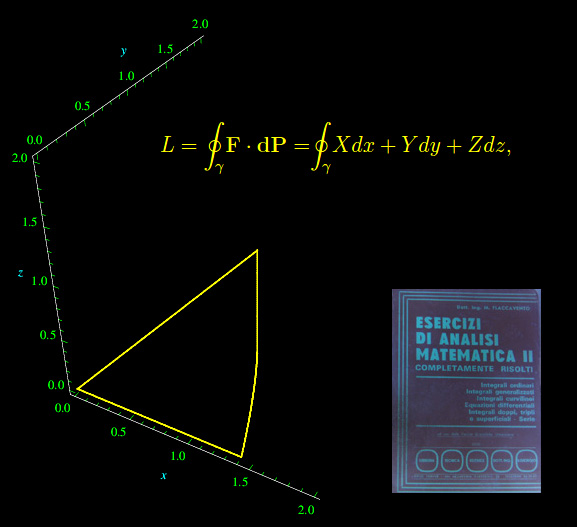

integrali curvilinei,flaccavento,lavoro di una forza,differenziale esatto — **Fig. 1**.

Esercizio n.7, pag. 78 del Flaccavento
Calcolare il lavoro svolto dal campo di forze

lungo la curva γ unione dei seguenti archi:

Soluzione
Il lavoro meccanico svolto dalla forza F è

dove X,Y,Z sono le componenti cartesiane della forza. Verifichiamo innanzitutto se la forma differenziale che compare nell'integrando è un differenziale esatto. Abbiamo

per cui dobbiamo calcolare manualmente l'integrale. Siccome il cammino di integrazione è l'unione di un numero finito di archi regolari (fig. 1), procediamo per decomposizione

dove

Iniziamo con L₁

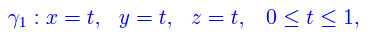
per cui

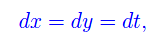
quindi

Cioè il primo percorso dà contributo nullo. Passiamo al secondo:

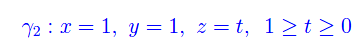
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Ciò implica

Passiamo al terzo:

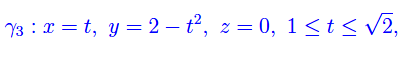
ovvero un arco di parabola contenuto nel piano coordinato xy:

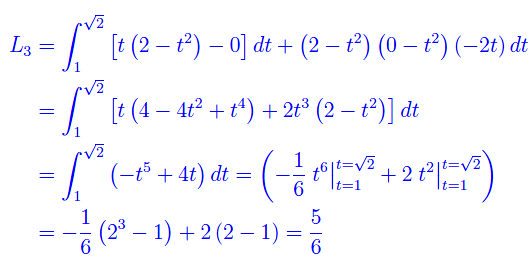
È facile verificare che L₄=0. Conclusione

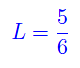
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Indice degli esercizi del Flaccavento

No TweetBacks yet. (Be the first to Tweet this post)