» Esercizi svolti di Matematica e Fisica

[¯|¯] Spazio delle configurazioni di un sistema lineare

Giugno 16th, 2018 | by Marcello Colozzo |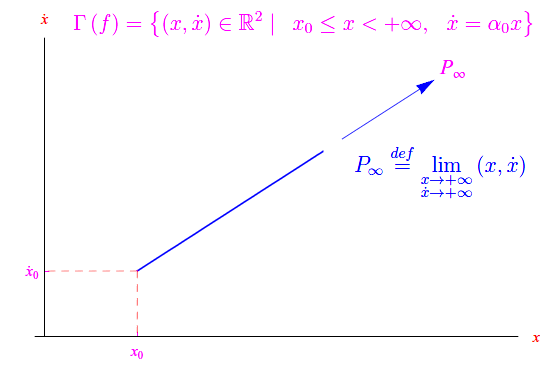

Applichiamo le nozioni precedenti ai sistemi autonomi lineari (del primo ordine), rammentando che

e

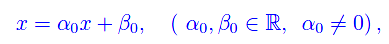
0=0) e non omogeneo (ß₀=/0). Per quanto visto in precedenza l'integrale generale per ß₀=0 è

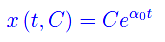
Dopo aver posto t₀=0, consideriamo la condizione iniziale

onde

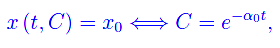
da cui l'integrale particolare che verifica il predetto problema di Cauchy:

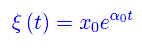
Introduciamo la grandezza

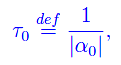
avente le dimensioni di un tempo e che si chiama costante di tempo del sistema. Ne consegue:

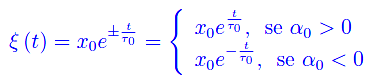
Abbiamo, dunque, una crescita esponenziale per α₀>0 e una decrescita esponenziale per α₀<0. In fig. eq:traiettoria_p1 riportiamo il grafico di ξ(t) per α₀>0 e per differenti valori della costante di tempo.

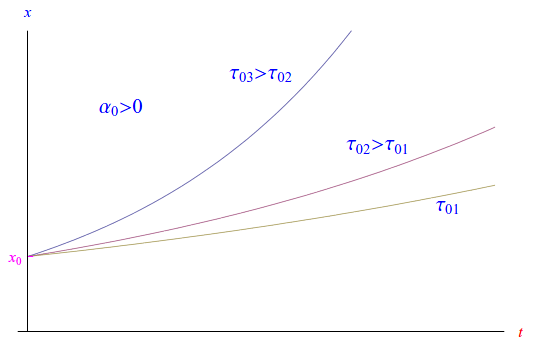
La regione dello spazio delle configurazioni accessibile per il sistema autonomo lineare ed omogeneo assegnato, è

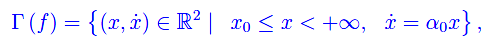
come illustrato nelle figg. seguenti

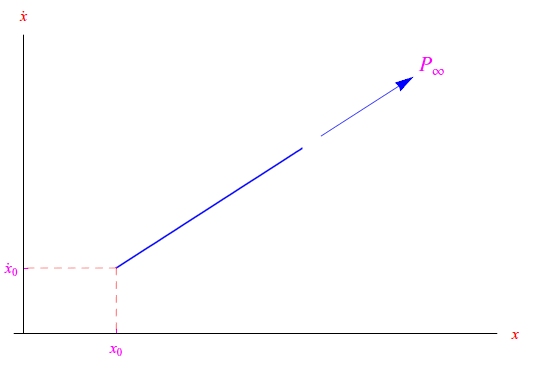
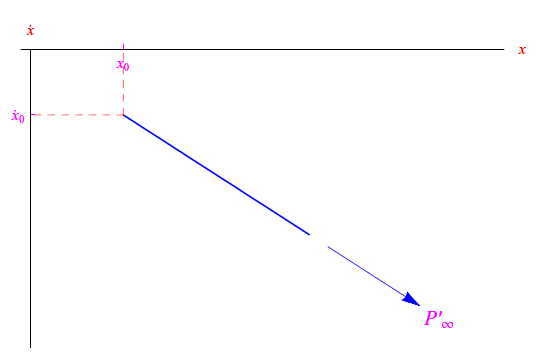
In entrambi i casi il sistema evolve deterministicamente a partire dallo stato iniziale ((x₀,α₀x0)). In simboli:

dove

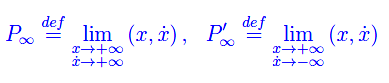
Tags: sistemi dinamici autonomi, sistemi lineari, spazio delle configurazioni

Articoli correlati