[¯|¯] Il problema delle condizioni iniziali. Problema di Cauchy. Funzioni lipschitziane

Giugno 10th, 2018 | by Marcello Colozzo |

Un ulteriore indizio che lega la nozione di autopoiesi di Maturana-Varela al cosiddetto "pensiero sistemico" elaborato verso la fine degli anni Quaranta da un gruppo di matematici e fisici che si riunivano periodicamente nelle conferenze della Macy, è riportato nel libro "La rete della vita" (fig. 1) del fisico F. Capra. Nel brano in questione si parla, appunto, di automi cellulari che come è noto, vennero elaborati da J. Von Neumann, quale matematico e membro delle predette conferenze.

Gli automi cellulari sono sistemi deterministici: lo stato a tutti i tempi di un automa, è univocamente determinato dal suo stato iniziale. Nel nostro linguaggio che stiamo portando avanti da un paio di post, ciò si traduce nel noto Teorema di Cauchy-Lipschitz o Teorema di esistenza ed unicità. Per essere più speficici, riprendiamo il sistema autonomo:

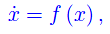
L'integrale generale di tale equazione differenziale è definito a meno di una costante di integrazione. Tuttavia a noi interessa l'evoluzione dinamica del sistema i.e. la funzione x(t), a partire da un istante iniziale t₀, in cui è x(t₀)=x₀ valore noto.

Matematicamente ciò è formulato dal seguente problema di Cauchy

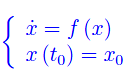
Come è noto dalla teoria delle equazioni differenziali, una condizione sufficiente affinché tale problema sia compatibile e determinato, è che la funzione f(x) sia lipschitziana.

In precedenza avevamo richiesto la continuità di f(x) e della sua derivata prima. Tale condizione può essere indebolita, richiedendo la sola lipschitzianità che garantisce la continuità. Infatti, la lipschitzianità è una condizione sufficiente per la continuità uniforme e, quindi, per la continuità puntiforme (cioè l'usuale continuità).

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.