[¯|¯] Coordinate polari nel piano

Maggio 25th, 2018 | by Marcello Colozzo |

Sia α un piano su cui è assegnato un riferimento cartesiano R(Oxyz).
Definizione
Dicesi verso positivo delle rotazioni, il verso secondo cui deve ruotare l'asse x attorno all'origine O per sovrapporsi all'asse y, con una rotazione di π/2. Il verso negativo delle rotazioni è il verso opposto a quello positivo.

È facile convincersi che in un usuale riferimento cartesiano R(Oxyz), il verso positivo è quello antiorario, come illustrato in figura:

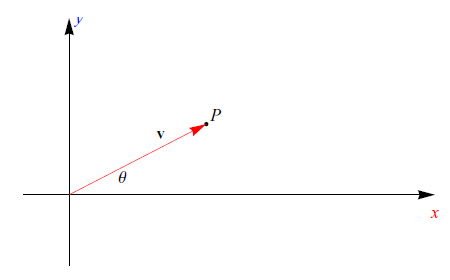
Assegnato un punto P di un piano orientato, distinto dall'origine O del relativo riferimento cartesiano R, consideriamo il vettore posizione di P ovvero il vettore r applicato in O e di estremo P:

Definizione
Il vettore r si dice vettore posizione del punto P.
Denotiamo con ρ il modulo di r:
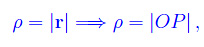
coordinate polari nel piano,raggio vettore,anomalia

essendo |OP| la misura assoluta del segmento OP. Chiamiamo θ la misura relativa di uno degli angoli di cui deve ruotare l'asse x per sovrapporsi al vettore posizione r. Cioè

Tale rotazione è manifestamente definita a meno di multipli interi di 2π, onde se θ₀ è la misura relativa dell'angolo che definisce una particolare rotazione, dovrà aversi:

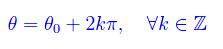
Definizione
La coppia ordinata (ρ,θ) definisce le coordinate polari del punto P. I numeri reali ρ,θ sono rispettivamente il raggio vettore e l'anomalia di P.
In tal modo è univocamente definito un riferimento polare (o sistema di coordinate polari) costituito dal polo O e dall'asse polare coincidente con l'asse x.

Per quanto precede, l'anomalia è definita a meno di multipli interi di 2p, conformemente all'equazione vista più sopra.
Definizione
Il valore assunto da θ per un particolare valore di k, si dice determinazione dell'anomalia. L'anomalia principale di P è:

Concludiamo, ricavando (tramite la fig. al top) le equazioni di trasformazione che collegano le coordinate cartesiane alle coordinate polari. Precisamente: