[¯|¯] Piano osculatore e cerchio osculatore

Settembre 27th, 2017 | by Marcello Colozzo |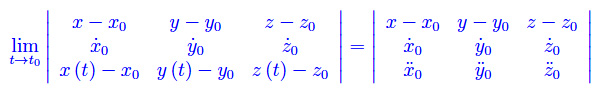

piano osculatore,cerchio osculatore,curva regolare

Sia data la curva regolare Γ con rappresentazione parametrica:

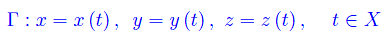
Fissiamo su Γ un punto P₀=P(t₀)tale che ρ(M₀)=2, dove M₀ è la matrice
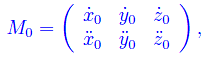
piano osculatore,cerchio osculatore,curva regolare

avendo denotato con la notazione puntata l'operazione di derivazione rispetto a t. Per una nota proprietà il punto P₀ è punto di curvatura per Γ. Se t₀ è la retta tangente a Γ in P₀, la sua equazione si scrive:

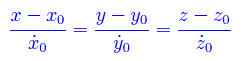
Manifestamente si ha

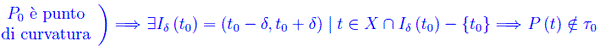
Preso ad arbitrio uno di tali punti, cioè

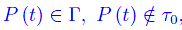
esiste ed è unico il piano ω(t) contenente la retta t₀ e passante per P(t):
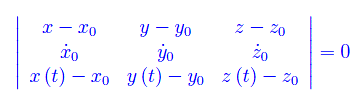
piano osculatore,cerchio osculatore,curva regolare

Nel determinante a primo membro le variabili reali x,y,z sono le coordinate cartesiane del generico punto di ω(t)s, mentre le x(t),y(t),z(t) sono le coordinate cartesiane del punto di Γ distinto da P₀.

continua in pdf

Sostienici

No TweetBacks yet. (Be the first to Tweet this post)