[¯|¯] Oscillazioni smorzate. Il caso critico (oscillatore criticamente smorzato)
Marzo 20th, 2017 | by Marcello Colozzo |
Fig. 1. Evoluzione nello spazio delle configurazioni dello stato meccanico di un oscillatore criticamente smorzato, per differenti valori della posizione iniziale.
Caso critico (b=bcrit)
L'equazione caratteristica ha una sola radice reale:

per cui un sistema di integrali fondamentali è

Pertanto l'integrale generale dell'equazione differenziale dell'oscillatore armonico smorzato si scrive:

Derivando otteniamo la velocità
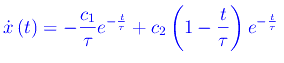
Imponendo le condizioni iniziali

si perviene al sistema:

da cui
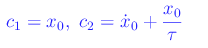
Quindi l'integrale particolare che ci interessa è:

e la velocità
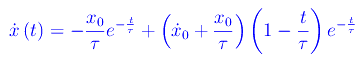
Assumendo una velocità iniziale nulla le equazioni precedenti si scrivono:
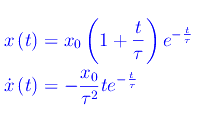
A differenza del caso aperiodico dove intervenivano due costanti di tempo τ1,τ2, la scala dei tempi del transitorio è fissata dall'unica costante di tempo τ=(2m)/b:

A rigore:

Osserviamo che la costante di tempo è ora legata alla pulsazione caratteristica dall'evidente relazione:

Ad esempio, per ω0=20rad/s otteniamo per l'ascissa x(t) l'andamento riportato in figura:

in fig. 1 (top di questa pagina) è plottato il diagramma delle orbite.
Ne concludiamo che anche nel caso criticamente smorzato, il punto materiale non compie oscillazioni e l'ascissa dopo un transitorio di durata τ, l'ascissa si annulla.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: attrito, caso critico, oscillatore armonico smorzato, resistenza passiva
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











