» Esercizi svolti di Matematica e Fisica

[¯|¯] Preludio all'ergodicità

Marzo 12th, 2017 | by Marcello Colozzo |

---

Qui per "segnale" intendiamo una qualunque grandezza fisica y(t).
Definizione 1
Un segnale y(t) si dice processo deterministico (o semplicemente deterministico) se la funzione y(t) è l'unica soluzione di un assegnato problema di Cauchy:

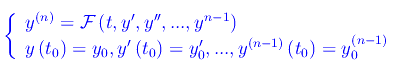
La n-pla

si dice stato iniziale del segnale.

Denotiamo con y_det(t) un qualunque segnale deterministico. Per quanto precede, lo stato iniziale di tale segnale determina univocamente lo stato a tutti i tempi.
Definizione 2
Un segnale y(t) si dice processo aleatorio (o semplicemente aleatorio) se esiste un processo deterministico P(y,t) rispetto alla variabile t, tale che P(y,t') è la probabilità che al tempo t' il segnale assuma il valore y(t'). Più precisamente, P(y,t) è una densità di probabilità, nel senso che P(y0,t)dy è la probabilità infinitesima che una misura di y all'istante t fornisca un valore appartenente all'intervallo infinitesimo [y0,y0+dy].
Segue che P(y,t) è l'unica soluzione di un assegnato problema di Cauchy:

dove γ₀ è una curva regolare contenua nel campo di esistenza di P(y,t) di rappresentazione parametrica x=α(t),y=ß(t),t in [t1,t2], e φ(t),η(t) funzioni assegnate appartenenti a C¹([t1,t2]).
Esempio 1
Si consideri una particella classica che si muove lungo l'asse x sotto l'azione di una forza di modulo F(t,x,x). Per la seconda legge di Newton:

dove il secondo membro è la forza per unità di massa. Abbiamo quindi il problema di Cauchy:

Se la funzione f è continua nel suo insieme di definizione ed è ivi lipschitziana rispetto alle variabili x,x, segue che il predetto problema di Cauchy è compatibile e determinato.

Conclusione: l'ascissa di una particella classica che si muove sotto l'azione di un campo lipschitziano è un segnale deterministico.
Esempio 2
Si consideri una particella quantistica che si "muove" lungo l'asse x sotto l'azione di un campo di energia potenziale V(x,t), per cui la funzione d'onda della particella è soluzione dell'equazione di Schrödinger:

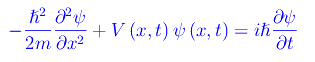
La densità di probabilità è

precisamente:

è la probabilità di trovare la particella nell'intervallo [a,b] dell'asse x, i.e. la probabilità che una misura dell'ascissa fornisca un valore x appartenente all'intervallo [a,b]. Dal momento che la densità di probabilità &rho(x,t) è l'unica soluzione di un assegnato problema di Cauchy, ne concludiamo che l'ascissa di una particella quantistica è un segnale aleatorio.
Osservazione Da un punto di vista formale, un segnale deterministico è un segnale aleatorio con probabilità identicamente uguale a 1.

Comunque prendiamo un segnale aleatorio y_al(t) a cui è associata la probabilità P(y,t), il valor medio diy_al(t) al generico istante t è per definizione dato da:

essendo T l'insieme dei valori assunti da y. Senza perdita di generalità supponiamo che y vari con continuità da -oo a +oo, onde:

Di particolare interesse (in quanto più diffusi) sono i processi aleatori stazionari, per i quali la densità di probabilità non dipende esplicitamente dal tempo:

In tal caso, il valor medio di y non dipende dal tempo:

In tale ipotesi è utile introdurre la nozione di insieme statistico o ensamble. Tale insieme è definito da tutti i valori assunti da un segnale aleatorio y_al(t) caratterizzato dallo stato iniziale

dove

Qui Γ è lo spazio delle fasi per la grandezza y_al(t), mentre la n-pla

definisce le coordinate del punto rappresentativo nello spazio delle fasi.
Definizione 3

Il processo aleatorio y_al(t) è ergodico se dopo un tempo sufficientemente lungo il suo punto rappresentativo ricopre l'intero spazio delle fasi.

Da questa definizione segue che la media temporale:

si identifica con la media di ensamble:

Cioè

Tags: processi ergodici, processi stazionari, segnali aleatori, segnali deterministici

Articoli correlati