[¯|¯] Ascissa curvilinea su una curva regolare orientata. Elemento d'arco. Rappresentazione naturale di una curva

Novembre 12th, 2016 | by Marcello Colozzo |

ascissa curvilinea,lunghezza arco di curva,equazioni parametriche

Fig. 1. Arco di cicloide


Nello spazio euclideo R³ consideriamo una curva regolare γ di rappresentazione parametrica:
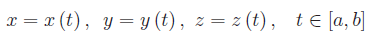
ascissa curvilinea,lunghezza arco di curva,equazioni parametriche
Su γ fissiamo un punto O(x0,y0,z0) con

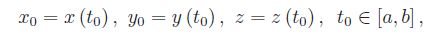
ascissa curvilinea,lunghezza arco di curva,equazioni parametriche
e un verso positivo, per cui γ è una curva regolare orientata.








Comunque prendiamo un punto P[x(t),y(t),z(t)], è univocamente definita la lunghezza dell'arco di curva di estremi O e P. Dalla geometria differenziale sappiamo che tale lunghezza è
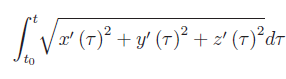
ascissa curvilinea,lunghezza arco di curva,equazioni parametriche
Ciò premesso, definiamo la funzione:

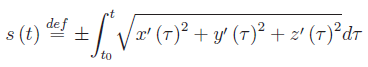
ascissa curvilinea,lunghezza arco di curva,equazioni parametriche

Continua a leggere in pdf

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , ,

Articoli correlati

  1. 1 Trackback(s)

  2. Nov 13, 2016: [¯|¯] Ascissa curvilinea sul grafico di una funzione reale di una variabile reale | » Matematica Open Source

Commenta l'esercizio