Caduta libera di una pallina (cinematica del punto materiale) |

Caduta libera di una pallina (cinematica del punto materiale)

Ottobre 25th, 2016 | by Marcello Colozzo |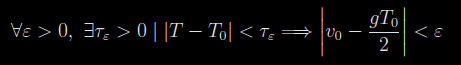

Un matematico tenta di determinare in funzione del tempo la coordinata y di una pallina che si muove verticalmente dopo che le è stata impressa una velocità iniziale v₀ verso l'alto, misurando il tempo di volo T (cioè il tempo di andata e ritorno) e il tempo t_max in cui la pallina nella fase ascendente raggiunge la massima quota per poi invertire il moto. Il matematico osserva che per T∈(T₀-τ_ε,T₀+τ_ε) dove T₀ è un valore assegnato del tempo di volo e τ_ε≪T₀, la velocità iniziale verifica la seguente limitazione:

|v₀-((gT₀)/2)|<ε (1)

essendo g=9.81m /s⁻² l'accelerazione di gravità. Facendo la ragionevole ipotesi che T sia una funzione continua di v₀, dimostrare a partire dalla (1) che

T=(2v₀)/g

Tenendo conto di tale risultato e che la derivata di y(t) si annulla in T/2 è possibile determinare l'espressione analitica della funzione y(t) (cioè l'equazione oraria del moto)?
Scarica la soluzione in formato pdf

No TweetBacks yet. (Be the first to Tweet this post)