[¯|¯] Le funzioni trigonometriche sinx e cosx

Dicembre 8th, 2014 | by extrabyte |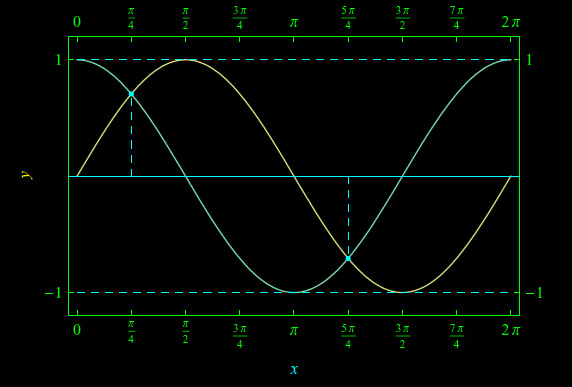

Prima di eseguire lo studio delle cosiddette funzioni trigonometriche (o funzioni circolari), premettiamo un ripasso delle nozioni fondamentali di trigonometria piana. Siano r e s due rette orientate complanari e formanti un angolo acuto.

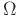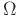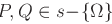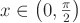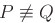Detto il punto di intersezione, denotiamo con x la misura inradianti dell'angolo acuto , onde . Comunque prendiamo con , restano univocamente definite le proiezioni ortogonali P' e Q' su r. I triangoli 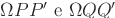sono simili, pertanto scriviamo

Assegnato il punto 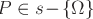, al variare di Q su 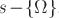, restano definiti oo triangoli rettangoli 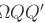aventi un vertice in 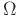e l'ipotenusa su s, la cui lunghezza è . Tali triangoli compongono l'insieme: