[¯|¯] Esercizio sulle funzioni inverse (parte 2)
Ottobre 6th, 2014 | by extrabyte |Studiare l'invertibilità della funzione:
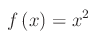
Svolgimento
Il campo di esistenza della funzione assegnata è il campo reale. Il suo grafico è la parabola y=x^2 ed è facile convincersi che la funzione non è strettamente monotona, onde non invertibile. Però è localmente monotona in senso stretto. Precisamente, risulta strettamente crescente in A=[0,+oo) e strettamente decrescente in B=(-oo,0].
Ne consegue che f è localmente invertibile. Per
determinare le inverse locali, risolviamo l'equazione algebrica sul campo reale:
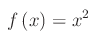
Tale equazione è compatibile se e solo se y>=0, per cui il codominio della funzione è f(X)=[0,+oo). Quindi, assegnato y>=0, risulta:
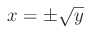
Da ciò si deduce che le inverse locali sono:
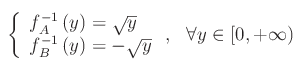
Il grafico della funzione è riportato in fig. 1.
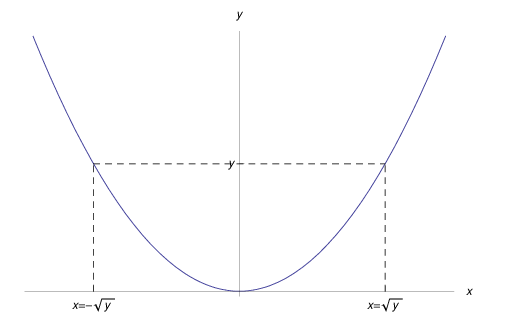
Fig. 1.

Tags: equazione algebrica, funzione inversa, funzione localmente invertibile, inversa locale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











