[¯|¯] Esercizio sulle funzioni monotone
Settembre 27th, 2014 | by extrabyte |Studiare la monotonia delle funzioni:
1) 
2) ![f\left( x\right) =\left[ x\right]](https://www.extrabyte.info/wp-content/plugins/latex/cache/tex_2878646a1f5dd8601b6f101cd77d9675.gif)
3) ![f\left( x\right) =x-\left[ x\right]](https://www.extrabyte.info/wp-content/plugins/latex/cache/tex_abc8ae98065e7cbad28317bcdb52a305.gif)
Tenendo conto del grafico della funzione  riportato in fig. 1 e della definizione di
riportato in fig. 1 e della definizione di
funzione monotona, vediamo che  non è monotona in
non è monotona in  , ma lo è localmente. Infatti, posto
, ma lo è localmente. Infatti, posto  e
e ![B=\left(-\infty,0\right]](https://www.extrabyte.info/wp-content/plugins/latex/cache/tex_2aea780d9e69143ecab718799adf5e0e.gif) , si ha che
, si ha che  è strettamente crescente e
è strettamente crescente e  è strettamente decrescente. Ne concludiamo che
è strettamente decrescente. Ne concludiamo che  è strettamente crescente in
è strettamente crescente in  e strettamente decrescente in
e strettamente decrescente in  .
.
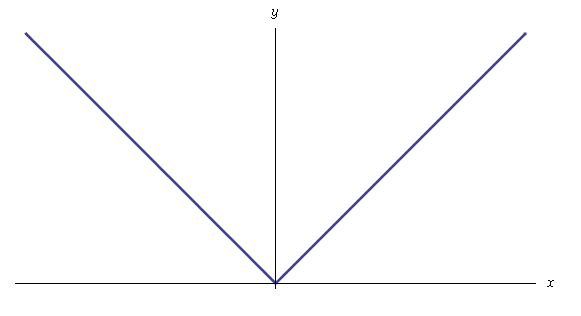
Fig. 1.
Dal grafico di ![f\left( x\right) =\left[ x\right]](https://www.extrabyte.info/wp-content/plugins/latex/cache/tex_866ad4253a17038b8d25855f8d0ceb78.gif) vediamo che tale funzione è crescente nel suo insieme di definizione. Quindi la funzione parte intera di
vediamo che tale funzione è crescente nel suo insieme di definizione. Quindi la funzione parte intera di  è monotona (ma non in senso stretto).
è monotona (ma non in senso stretto).
3) ![f\left( x\right) =x-\left[ x\right]](https://www.extrabyte.info/wp-content/plugins/latex/cache/tex_6b89eca5d655b40570a9b1e952d71f89.gif) . Anche qui è
. Anche qui è  .
.
Si ottiene facilmente:
\begin{align}
n & =1\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 0,1\right) \Longrightarrow f\left( x\right) =x\\
x\in\left( -1,0\right] \Longrightarrow f\left( x\right) =x
\end{array}
\right. \\
n & =2\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 1,2\right) \Longrightarrow f\left( x\right) =x-1\\
x\in\left( -2,-1\right] \Longrightarrow f\left( x\right) =x+1
\end{array}
\right. \nonumber\\
n & =3\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 2,3\right) \Longrightarrow f\left( x\right) =x-2\\
x\in\left( -3,-2\right] \Longrightarrow f\left( x\right) =x+2
\end{array}
\right. \nonumber\\
& ...\nonumber
\end{align}
Da ciò segue che il grafico della funzione ha l'andamento illustrato in fig. 2.
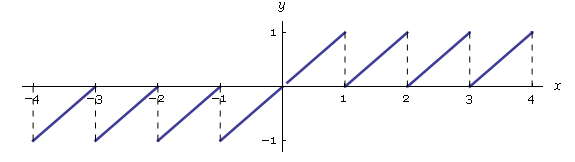
Fig. 2.
Inoltre  , dove:
, dove:

Abbiamo, cioè, una partizione di  , e
, e  è strettamente crescente in ogni
è strettamente crescente in ogni  , \
, \ ![\left( -n,-n+1\right]](https://www.extrabyte.info/wp-content/plugins/latex/cache/tex_48746c65646bcff56ebc3bd1612abfa0.gif) . Ne concludiamo che la funzione proposta è strettamente crescente a tratti.
. Ne concludiamo che la funzione proposta è strettamente crescente a tratti.

Tags: funzione parte intera di x, funzione valore assoluto, funzioni crescenti, funzioni decrescenti, funzioni monotone
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











