[¯|¯] La funzione parte intera di x

Settembre 18th, 2014 | by extrabyte |

funzione parte intera,integerpart — **Fig. 1**

Rammentiamo la definizione di parte intera di un numero reale. Assegnato un qualunque numero reale x, scriviamone la rappresentazione decimale:

dove p è un intero naturale assegnato, mentre c_k appartengono all'insieme {0,1,...,9}.

Poniamo per definizione:
\begin{equation}
\left[ x\right] \overset{def}{=}\pm p
\end{equation}
Cioè denotiamo con la parte intera di . Ciò premesso, la funzione parte intera di è:
\begin{equation}
\underset{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\longrightarrow\left[x\right] ,\,\,\,\,\forall x\in\mathbb{R}}{f:\mathbb{R}\rightarrow\mathbb{Z}%},\label{eq: funzione_parte_intera}%
\end{equation}
Se 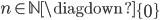, si ha:
\begin{align*}
x & \in\left[ n-1,n\right) \Longrightarrow\left[ x\right] =n-1\\
x & \in\left( -n,-n+1\right] \Longrightarrow\left[ x\right] =-n+1
\end{align*}
Esplicitiamo alcuni valori di :
\begin{align*}
n & =1\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 0,1\right) \Longrightarrow\left[ x\right] =0\\
x\in\left( -1,0\right] \Longrightarrow\left[ x\right] =0
\end{array}
\right. \\
n & =2\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 1,2\right) \Longrightarrow\left[ x\right] =1\\
x\in\left( -2,-1\right] \Longrightarrow\left[ x\right] =-1
\end{array}
\right. \\
n & =3\Longrightarrow\left\{
\begin{array}
[c]{l}%
x\in\left[ 2,3\right) \Longrightarrow\left[ x\right] =2\\
x\in\left( -3,-2\right] \Longrightarrow\left[ x\right] =-2
\end{array}
\right. \\
& ...,
\end{align*}

da cui segue che il grafico è l'unione di un numero infinito di segmenti. Precisamente il segmento aperto 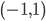, infiniti segmenti semiaperti a destra e infiniti segmenti semiaperti a sinistra.
Riportiamo il grafico in fig. 1, da cui vediamo che si proietta sull'asse nell'insieme di definizione della funzione e sull'asse nel codominio .

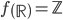La funzione parte intera è utilizzata in molti linguaggi di programmazione ed è implementata in molti sistemi di computer algebra (C.A.S.). In Mathematica, ad esempio,è data da IntegerPart[]. La funzione built-in che viene invocata dal comando Floor[] riproduce gli stessi
risultati di IntegerPart[] solo per 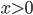. In fig 2
riportiamo il grafico della funzione Floor[x].