[¯|¯] Successioni univocamente definite. Successioni ricorsivamente definite. I numeri di Fibonacci

Settembre 14th, 2014 | by extrabyte |

ATTENDERE IL CARICAMENTO DELLA PAGINA PER LA CORRETTA VISUALIZZAZIONE DELLE FORMULE

Nella lezione precedente abbiamo definito il concetto di funzione reale di una variabile reale, quale applicazione tra due sottoinsiemi di $\mathbb{R}$ che abbiamo denotato con $X$ e $Y$ :

$f:X\rightarrow Y$

Un caso particolare di funzione reale di una variabile reale è quello in cui

$X=\mathbb{N}$ , dove

$\mathbb{N}=\left\{ 0,1,2,...,n,...\right\}$ è l'insieme degli interi naturali. Una tale funzione è detta
successione. Più precisamente:
Definizione 1
Assegnato

$Y\subseteq\mathbb{R}\mid$

$Y\not =\emptyset$ , dicesi successione di elementi di

$Y$ , una funzione:
\begin{equation}
\underset{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n\longrightarrow y\left( n\right) ,\,\,\ \,\forall n\in X}{y:\mathbb{N}\rightarrow Y}
\label{eq: succ}%
\end{equation}
La numerabilità di

$\mathbb{N}$ implica la numerabilità del codominio di

$y$ , cioè dell'insieme

$y\left( \mathbb{N}\right) \subset\mathbb{R}$ .
Infatti:

$y\left( \mathbb{N}\right) =\left\{ y\left( 1\right) ,y\left( 2\right),...,y\left( n\right) ,...\right\}$

Siccome la variabile indipendente è l'intero naturale

$n$ , è preferibile denotare con

$y_{n}$ il valore

$y\left( n\right)$ , che si chiama termine n-esimo della successione. Si utilizza, poi, la
notazione compatta:

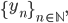
$\left\{ y_{n}\right\} _{n\in\mathbb{N}},$

che può essere ulteriormente snellita:

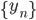
$\left\{ y_{n}\right\}$

Esercizio
Determinare il codominio della successione il cui termine n-esimo è 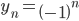$y_{n}=\left( -1\right) ^{n}$ .

Svolgimento.

Esplicitiamo i singoli termini:

$y_{0}=1,\,\,y_{1}=-1,\,\,y_{2}=1,\,\,y_{3}=-1,...,$

onde

$y\left( \mathbb{N}\right) =\left\{ -1,1\right\}$ . Ne concludiamo che

$\left\{ \left( -1\right) ^{n}\right\}$ è una successione di elementi di

$\left\{ -1,1\right\}$ .

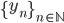L'univocità della corrispondenza (\ref{eq: succ}) implica che la successione di elementi di $Y$ che abbiamo denotato con $\left\{y_{n}\right\} _{n\in\mathbb{N}}$ è univocamente definita. Di contro, esistono successioni ricorsivamente definite, nel senso che il termine n-esimo dipende dai termini precedenti. Cioè:

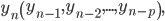
$y_{n}\left( y_{n-1},y_{n-2},...,y_{n-p}\right) ,$

dove

$p\in\left\{ 1,2,...,n-1\right\}$ . Un esempio è dato dalla successione di Fibonacci:
\begin{equation}
y_{n}=y_{n-1}+y_{n-2},\,\,\,\,\,n\in\mathbb{N}\diagdown\left\{ 0,1\right\}
\label{eq: fibo}%
\end{equation}
Per poter determinare i termini (denominati numeri di Fibonacci) della successione (\ref{eq: fibo}), è necessario conoscere

$y_{0},\,y_{1}$ che sono:

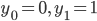
$y_{0}=0,\,\,y_{1}=1$

Quindi:
\begin{align*}
y_{2} & =y_{1}+y_{0}=1+0=1\\
y_{3} & =y_{2}+y_{1}=1+1=2\\
y_{4} & =y_{3}+y_{2}=2+1=3\\
y_{5} & =y_{4}+y_{3}=3+2=5\\
y_{6} & =y_{5}+y_{4}=5+3=8\\
& ...
\end{align*}
Cioè, il codominio della successione di fibonacci è:

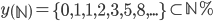
$y\left( \mathbb{N}\right) =\left\{ 0,1,1,2,3,5,8,...\right\}\subset\mathbb{N}%$