[¯|¯] Programmi ricorsivi con Mathematica

Agosto 29th, 2014 | by extrabyte |

Impariamo ad utilizzare una tecnica di casching nella ricorsione con Mathematica

Quando si scrivono programmi ricorsivi con Mathematica può essere utile utilizzare una tecnica di cahing, ovvero di memorizzazione dei valori calcolati. Prima di illustrare tale tecnica introduciamo il comando Table[] e la funzione built-in Prime[] che restituisce l'n-esimo numero primo. Table[] è un generatore di liste e la sua sintassi è Table[<espressione>, {k,kmin,kmax,kstep}]. In questo costrutto k è un iteratore che prende valori nell'intervallo discreto kmin, kmax, mentre kstep assegna il passo. Per default è kmin=kstep=1. Cioè, se scriviamo Table[<espressione>, {k,kmax}], Mathematica restituisce i valori assunti da expr per kstep variabile da 1 a kmax con passo 1.
Ciò premesso, definiamo la seguente funzione ricorsiva:

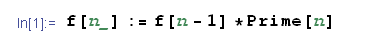
Il valore assunto da tale funzione in n=0 sia:

Qui abbiamo fatto uso del terminatore ; che impedisce la visualizzazione dell'output. Utilizziamo il comando Table per determinare i valori assunti da f in un assegnato intervallo discreto. Abbiamo così generato una successione per ricorsione (si pensi ai numeri di Fibonacci).

Ad esempio:

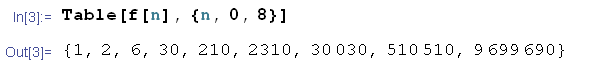
La tecnica cashing, in questo caso, consiste nel combinare le definizioni di funzione utilizzate da Mathematica. Precisamente, la cosiddetta assegnazione ritardata e l'assegnazione immediata.

Nell'assegnazione ritardata la funzione viene valutata solo quando viene richiamata dall'utente. La sintassi è f[x_]:=espressione. Viceversa, nell'assegnazione immediata la funzione viene valutata subito. La sintassi è f[x_]=espressione.

Nel caso in esame scriviamo:

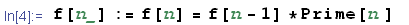
Analizziamo questo costrutto. L'istruzione f[n] = f[n-1] * Prime[n] restituisce il valore richiesto, cioè f[n] che, al tempo stesso viene memorizzato dal kernel grazie all'assegnazione ritardata f[n_]:= f[n]. Fatto ciò, possiamo dare in pasto f[b] al comando Table[] per calcolare i valori assunti dalla funzione ricorsiva in un intervallo assegnato.